Vlak voordat vrijdag de gebeurtenissen in Noorwegen het nieuws domineerden, stond er een kop op nu.nl: ‘Extreme klimaatverandering mogelijk’
UTRECHT – De hoeveelheid koolstof die wij met zijn allen uitstoten, zou wel eens kunnen leiden tot een extreme verandering van het klimaat, met een wereldwijde uitroeiing van verschillende dier- en plantsoorten als gevolg.
Het blijkt te gaan over een publicatie over de massa-uitsterving op het einde van het Trias-tijdperk, waar meer dan 20% van de soorten het niet overleefde. (zie wikipedia voor achtergrondinformatie). De publicatie is een offspin van de promotie van Micha Ruhl aan de afdeling paleoecologie van de universiteit van Utrecht: Carbon Cycle Changes during the Triassic-Jurassic Transition” (Januari 2010)
De claims in het nieuwsbericht zijn overtrokken, zoals tegenwoordig gebruikelijk is met klimaatnieuws.
Publicatie
Hier is het abstract van de publicatie waar het allemaal om gaat in het nieuwsbericht:
Atmospheric carbon injection linked to end-Triassic mass extinction.
Abstract
The end-Triassic mass extinction (~201.4 million years ago), marked by terrestrial ecosystem turnover and up to ~50% loss in marine biodiversity, has been attributed to intensified volcanic activity during the break-up of Pangaea. Here, we present compound-specific carbon-isotope data of long-chain n-alkanes derived from waxes of land plants, showing a ~8.5 per mil negative excursion, coincident with the extinction interval. These data indicate strong carbon-13 depletion of the end-Triassic atmosphere, within only 10,000 to 20,000 years. The magnitude and rate of this carbon-cycle disruption can be explained by the injection of at least ~12 × 10(3) gigatons of isotopically depleted carbon as methane into the atmosphere. Concurrent vegetation changes reflect strong warming and an enhanced hydrological cycle. Hence, end-Triassic events are robustly linked to methane-derived massive carbon release and associated climate change.
Ref:
Ruhl M, Bonis NR, Reichart GJ, Sinninghe Damsté JS, Kürschner WM., Atmospheric carbon injection linked to end-Triassic mass extinction. Science. 2011 Jul 22;333(6041):430-4. abstract
Opvallend is dat er in het abstract:
a) totaal geen link wordt gelegd naar het klimaat van vandaag
b) het hele proces van uitsterving tien- tot twintigduizend jaar in beslag nam: vergelijkbaar in snelheid dus met het einde van de laatste ijstijd.
c) vergelijk 12000 gigaton ook met de huidige fossiele 8 gigaton per jaar.
Methaan
De bangmakerij in het nieuwsartikel wordt gedaan op de basis van methaan dat tegenwoordig gevangen zit in toendra en ongeconsolideerde sedimenten en dat een opwarming dit methaan zou kunnen vrijmaken. Nu was de situatie tijdens het einde van het Trias totaal anders als tegenwoordig, zo waren er bijvoorbeeld geen poolkappen waardoor de zeewatertemperatuur ook al hoger was, zie dit paleoecologisch kaartje van Christopher Scotese (http://www.scotese.com):
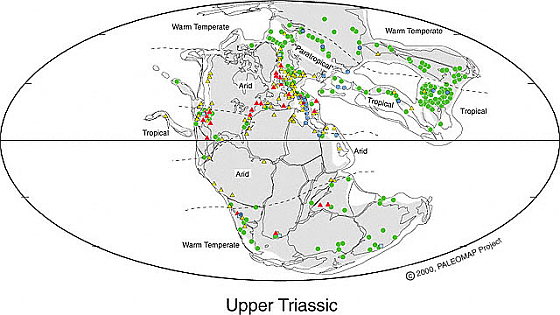
paleoklimaat aan het einde van het Trias (scotese.com) 'Global climate was warm during the Late Triassic. There was no ice at either North or South Poles. Warm Temperate conditions extended towards the poles'
De grote hoeveelheden methaan zaten dus toen niet in de toendrabodems, want die waren er gewoon niet.
conclusie
Ruhl et al hebben een goede studie gepresenteerd over de koolstofbalans tijdens de massauitsterving aan het einde van het trias, maar de draai die nu.nl er aan heeft gegeven, geeft niet weer wat de conclusies van het artikel zijn.
Links
Nederlands:
– nu.nl
– Volkskrant
– nieuws.nl
– Vroege Vogels
Engels:
– USAToday
– Science
– oi9.com
– sciencenews.org






@BenAW2
Lees nu pas (goed) dat je het broeikaseffect wilt wegschuiven omdat:
Na albedo 239 W/m^2 opgenomen door aarde EN atmosfeer.
Uitgaand 239 W/m^2, uitgestraald door aarde EN atmosfeer.
En dat dit een keurige balans is. Over die (gemiddelde) getallen zijn de ‘stralingsdeskundigen” het eens. Staat ook in het KT schema, dat het broeikaseffect illustreert.
Maar die uitstraling is die aan de TOP van de atmosfeer. Beschrijft niet wat er in de onderliggende 10 km gebeurt. En op die processen berust de veronderstelling van de consequenties van het broeikaseffect voor het oppervlak.
@Theo
Nog steeds begrijp ik niet goed je redenering dat er in de stilstaande kolom ergens arbeid geleverd zou kunnen worden. We zijn het er over eens dat we in de troposfeer een gemiddelde kolom van 15 C beneden en -50 C op 10 km hoogte hebben. Maar niet dat ‘geleiding’ de zaak isotermisch zou maken.
Neem een ijzerstaaf die aan één kant op 15 C wordt gehouden en aan de andere kant op – 50 C. Er ontstaat door de gehele staaf een temperatuurgradiënt, door geleiding. Pas als je de 15 C opwarming weghaalt zal de warmte-inhoud zich gelijkmatig over de staaf verspreiden. Maar in je luchtkolom blijft het ‘kacheltje’ (zie BenAW) aan.
In je betoog haal je de tropopauze erbij. Maar de productie van de temperatuurgradiënt als gevolg van de adiabatische expansie, loopt maar tot de tropopause. En die zal dus mijns inziens in stand blijven volgens de formules in de leerboekjes. dp/p = – dz/H waarin H= RT/g
en dT/dz = = -g/Cp
De redenering waarmede de leerboekjes de gradiënt verklaren berust op ‘parcels’ die kunnen stijgen of dalen. Het is een verklaring via de boyant density.
Laten we zo’n parcel verpakken in een Helium ballontje en aan het oppervlak loslaten. Het draagt wat warmte met zich mee. Bij stijging is het zelf onderhevig aan adiabatische expansie.Het zet uit en het Helium neemt de temperatuur van de omgeving aan. Laten we even aannemen dat het niet knapt. Dan blijft het met een zekere warmte-inhoud ergens in de troposfeer hangen als interne en externe druk aan elkaar gelijk zijn. Met de temperatuur van de ‘hang-hoogte’. De hoger liggende laag is kouder. Om die een beetje op te warmen met de warmte inhoud van het ballontje, zul je het een opwaartse kracht moeten meegeven. Dus arbeid toevoegen. Er wordt geen arbeid geproduceerd. In de tweede laag staat het zijn warmte weer af. Die wordt wat warmer, maar dat is dan het gevolg van de eerder toegevoegde arbeid.
Dit proces doet zich in werkelijkheid voor bij convectie, die dan de arbeid levert. Zie hoe een zweefvliegtuig gebruik maakt van de thermiek om tegen de zwaartekracht in te gaan.
Aldus denk ik dat je op een dwaalspoor bent geraakt door ‘geleiding’ in je redenering te brengen tussen een warmere(lagere) en koudere (hogere laag) zonder convectie. De drijvende kracht achter het in stand houden van de gradiënt is de boyant density, als gevolg van de aanwezig blijvende zwaartekracht.
Een voorbeeld (metafoor) uit mijn oude experimentele vakgebied, (moleculaire biologie) waarbij ultracentrifuges werden gebruikt om het gewicht van macromoleculen te bepalen en deze te concentreren. De centrifugebuis werd gevuld met een suikeroplossing. Onder invloed van de centrifugale kracht ontstaat er een gradiënt in de dichtheid van de suikeroplossing. Deze is laag aan de top van de buis, hoog aan de bodem. De macromoleculen hopen zich dan op in een smalle band, waarin hun dichtheid gelijk is aan die van de suikeroplossing. We stoppen dan de centrifuge. We moeten er vervolgens vrij snel bij zijn om die band af te tappen. Want na het wegvallen van de centrifugaalkracht zal de suikergradiënt verdwijnen en door diffusie de macromoleculen zich weer gaan verspreiden in de hele buis.
Met deze metafoor probeer ik aan te geven, dat het mij lijkt dat je alleen een troposfeer zonder temperatuurgradiënt kunt verwachten, als de zwaartekracht zou wegvallen.
@Arthur
We zijn het inderdaad eens dat er een adiabatische lapse rate is in de huidige atmosfeer.
Maar die is mijns inziens (en ook volgens het Wikipedia artikel) het gevolg van de uitstraling door broeikasgassen rond de tropopauze.
Die uitstraling is zó groot dat er een temperatuurverschil met het aardoppervlak ontstaat dat groot genoeg is om convectie toe te staan, en daaruit ontstaat een keurige adiabatic lapse rate, met als gevolg een tropopauze, en wel op de hoogte die volgt uit de hoeveelheid uitgestraalde energie. Bij méér broeikasgassen is er méér uitstraling en is er dus een hogere convectie en dus een hogere tropopauze.
Zonder broeikasgassen is er alleen uitstraling en absorptie op het aardoppervlak. Het eerstvolgende stralingseffect is opwarming door UV in de stratosfeer.
Volgens mij houdt dat in dat de luchttemperatuur vanaf het oppervlak met de hoogte aanvankelijk bijna gelijk blijft, door warmtegeleiding vanaf het oppervlak, maar naarmate hij dichter bij de troposfeer komt en ijler wordt, uiteindelijk begint op te warmen.
In een dergelijke atmosfeer is geen convectie mogelijk en zal zich dus ook geen ALR instellen.
Jij beweert dat de lapse rate er is door de zwaartekracht, en dat die er dus ook gewoon is als er géén broeikasgassen zouden zijn. Dan zou de atmosfeer dus ook dan eerst afkoelen met de ELR en daarna opwarmen, precies zoals nu.
Maar ik herhaal de vraag die je maar niet beantwoordt: hoe kan het dat er 80 graden temperatuurverschil is tussen de tropopauze en het oppervlak, en er volgens jou geen warmtetransport plaatsvindt? Dat gaat toch tegen de basiswetten van de natuurkunde in? Je kunt zelfs precies uitrekenen hoeveel dat warmtetransport is, en hoelang het duurt tot de temperatuur minder dan een graad verschilt.
Dat warmtetransport is er dus.
Als jij dan volhoudt dat het temperatuurverschil toch in stand blijft, is er blijkbaar een energiebron die dit compenseert door in de tropopauze precies zoveel warmte toe te voeren dat het temperatuurverschil in stand blijft.
Ik zou dus ook een thermokoppel bovenin de troposfeer kunnen hangen en er eindeloos energie uit kunnen winnen op het oppervlak als je gelijk hebt.
De kern van de vraag is dus: hoe schakel je de warmtegeleiding uit in jouw "model"?
@BenAW
Ik heb uitgelegd waarom Postma's formules niet kloppen. Niet met mijn berekeningen, niet met die van de andere sceptische deskundigen, en ook niet met die van de alarmistische deskundigen.
Er zit gewoon een aantoonbare denkfout in.
Dat kan ik theoretisch bewijzen, en empirisch aantonen, met miljoenen metingen met de in Delft gebouwde en door de hele wereld gebruikte Kipp&zn pyrgeometers.
Het ontkennen van back-radiation zonder onderbouwing maakt op mij dan ook geen erg deskundige indruk.
Dat Postma met een kloppend eindgetal schijnt te komen bewijst niets.
@Theo5
De tropopauze (met temperatuur -50C) is niet de ‘plaats’ waar de uitstraling naar het heelal plaats vindt. Zowel de uitgaande straling als de back radiation komen uit een laag met omvang. Bij wolkenloze hemel, de terugstraling voornamelijk tussen 1 en 0 km. Het merendeel van nog kleinere hoogte. De uitgaande straling die het heelal bereikt, begint bij 1 km. Met toenemende hoogte boven 3 km neemt die snel af omdat de emissietemperatuur snel afneemt, van -15C tot -50C.
De theoretische ‘atmosferische’ adiabaat is niet het gevolg van convectie, doch uitsluitend van de zwaartekracht g. Integendeel, de convectie verstoort de theoretische adiabaat, zodat een andere temperatuurgradiënt ontstaat dan in één zonder convectie (en zonder andere weerverschijnselen).
De convectie is niet het gevolg van een temperatuur verschil tussen bodem en top, maar van de drukgradiënt in de atmosfeer en het ‘gewicht’ van de massa die in beweging komt. Warme lucht is lichter dan koude. Daarom,bij de hoge oppervlakte temperatuur aan de equator is de convectie hoofdzakelijk opwaarts. Dat is de werking van de zogenaamde Hadley cell . Aan de pool is er overwegend een neerwaartse convectie van koude lucht. (Noemt men nu de polar cell). Daardoor ontstaan dagelijks aan de polen één of meer koude anticyclonen (hoge drukgebieden) die vervolgens zuidwaarts bewegen en ‘oplossen’ bij botsing op de warmere lucht nabij de keerkring.
Nogmaals, volgens de klassieke meteorologische leerboeken is de convectie van massa niet de oorzaak van de theoretische adiabaat, maar de verstoorder daarvan. Als je in de vorige post zegt “je beweert”, ik praat de leerboeken slechts na, en wel dat deel dat gevestigde klassieke meteorologie is.
Je zegt: “Maar ik herhaal de vraag die je maar niet beantwoordt: hoe kan het dat er 80 graden temperatuurverschil is tussen de tropopauze en het oppervlak, en er volgens jou geen warmtetransport plaatsvindt? Dat gaat toch tegen de basiswetten van de natuurkunde in? Je kunt zelfs precies uitrekenen hoeveel dat warmtetransport is, en hoelang het duurt tot de temperatuur minder dan een graad verschilt. Dat warmtetransport is er dus.
Als jij dan volhoudt dat het temperatuurverschil toch in stand blijft, is er blijkbaar een energiebron die dit compenseert door in de tropopauze precies zoveel warmte toe te voeren dat het temperatuurverschil in stand blijft.”
Ik meende dit, met de klassieke opvatting, te hebben uitgelegd. De ‘krachtbron’ is (in de stilstaande atmosfeer) de zwaartekracht. De primaire kracht voor het in stand houden van de drukgradiënt en die dan de adiabatische expansie opwekt met per definitie dQ/dt =0.
We kunnen de kwestie ook vanuit de tweede hoofdwet bekijken. In een afgesloten systeem wordt gestreefd naar maximale entropie. Als de kolom een gesloten systeem zou zijn, buiten invloed van externe krachten, zou dit leiden tot volledige homogenisatie (maximale wanorde). Maar het systeem is niet gesloten, (opnieuw) de g oefent zijn invloed uit.(‘potentiële’ energie) Daardoor wordt in de (stilstaande) kolom een zekere ‘orde’ gehandhaafd (het drukverschil) en treedt geen maximalisering van de entropie op. En ontstaat de adiabaat met dQ/dt =0.
De tweede hoofdwet wordt helaas nog steeds door velen (Postma o.a) vertaald als ‘warmte kan alleen van warm naar koud stromen”. Dat wordt uit de wet ‘afgeleid’, maar geldt alleen voor een gesloten systeem, zonder invloeden van buiten.
Ken je het gedachte-experiment van het duiveltje van Maxwell? Links een vat op een iets lagere temperatuur, rechts op iets hogere temperatuur, verbonden door een buis met daarin een kraan. Zet de kraan open en het eindresultaat is dat beide vaten op de zelfde temperatuur komen. Maar nu gaat het duiveltje van Maxwell de kraan bedienen (een invloed van buiten). Stuit op de kraan van links (koude ruimte) een molecuul met relatief hoge kinetische energie, dan draait het duiveltje de kraan open en laat het door naar de warme ruimte, die dus warmer wordt. Stuit op de kraan van rechts (warme ruimte) een molecuul met relatief lage kinetische energie, dan laat het duiveltje dit door naar de koude ruimte. Gevolg, de Maxwell verdeling in de warmte ruimte stijgt verder naar een hoger gemiddelde met als gevolg verdere temperatuur stijging. Tot dat in de koude ruimte alle moleculen met lage kinetische energie zijn verzameld en in de warme met hoge kinetische energie.
Dan over de tropopauze: hoe komt die tot stand? Waarom blijft de stratosfeer direct daarboven op hogere temperatuur en direct daaronder op lage temperatuur? Waarom stroomt hier warmte niet van warm naar koud en warmt de stratosfeer de troposfeer niet op?
Er is vrijwel geen ‘geleiding’ vanwege de geringe warmtecapaciteit van sterk verdunde lucht.
De stratosfeer en troposfeer blijven twee gescheiden werelden (1) door verschil in opwarming door de zon, (2) de weerverschijnselen zijn van heel andere aard. Het ‘ weer’ (met cyclonen en anticyclonen) speelt zich alleen in de troposfeer af, en het gebied waarin dit gebeurt, daarmee definieert men de hoogte van de tropopauze. Aan de tropen op 10 km (waar de diepe convectie soms doorheen breekt tot 18 km) aan de polen op een paar km hoogte. Je zou wellicht kunnen zeggen, de weersverschijnselen drukken de tropopauze omhoog (extreem bij diepe convectie), de van nature warmere stratosfeer naar beneden. Een ander soort ‘ duiveltje van Maxwell’ is dus aan het werk.
Met stralingsverschijnselen hebben deze processen weinig te maken, behalve dan dat de inkomende straling in de troposfeer van de zon, op mondiale schaal, qua energie-inhoud, in evenwicht zal zijn met IR uitstraling aan de top van de troposfeer, want warmte transport naar heelal met ‘ massa’ is niet mogelijk.
Tenslotte, je zegt “De kern van de vraag is dus: hoe schakel je de warmtegeleiding uit in jouw “model”? Het is niet ‘ mijn’ model maar klassieke meteorologie. Voorts in lucht, zelfs bij 1 atmosfeer, is de warmtegeleiding heel klein. Beperkt tot enige meters, de zogenaamde ‘ skin temperatuur’ van het oppervlak. Het is de g die de entropie laag en daarmee de ‘ orde’ hoog houdt.
Er is nog een andere oorzaak waarom de entropie niet maximaliseert, dat is het verschil in golflengte van inkomend zonlicht en uitgaande IR straling. Vergelijk het met een levende cel, die zich voedt met stoffen met hoge energie inhoud, en evenveel afvalproducten met lage produceert. Er loopt door de cel een voortdurende energiestroom, onder invloed van de zogenaamde thermodynamische potentiaal. In zo’n energetisch open systeem werkt de tweede hoofdwet even anders uit dan in een gesloten systeem en zal de entropie niet maximaliseren en blijft de informatie-inhoud (=orde) in de cel op peil. Voor het handhaven van de orde, is de warmtegeleiding van de levende cel naar de omgeving ook nauwelijks van betekenis. Tot dat de energie toevoer stopt. Dan gaat warmtegeleiding een heel langzame functie vervullen.En denatureren alle stoffen met hoge informatie-inhoud en maximaliseert de entropie. De entropiedood wordt dit in de biologie genoemd.
Aldus ontsnapt de troposfeer aan entropiedood, allereerst door hoog energetische zoninstraling, waarna de zwaartekracht het werk overneemt.
@Arthur
Eerste een directe reactie op een paar dingen die je schreef:
> Bij wolkenloze hemel, de terugstraling voornamelijk tussen 1 en 0 km. Het merendeel van nog kleinere hoogte.
Sterker nog, gemiddeld 93% uit de eerste ca 20 meter.
> De uitgaande straling die het heelal bereikt, begint bij 1 km. Met toenemende hoogte boven 3 km neemt die snel af omdat de emissietemperatuur snel afneemt, van -15C tot -50C.
Dat is in mijn ogen geen oorzaak maar gevolg, maar daarover later.
De uitstraling naar het heelal gebeurt vanaf een hoogte waarop de vrije weg van een IR foton langer is dan de resterende atmosfeer.
Deze verschilt in de huidige atmosfeer enorm tussen CO2 en H2O, omdat de CO2 concentratie weliswaar lager is en afneemt met de dichtheid van de atmosfeer, maar dat die van waterdamp véél sterker afneemt door condensatie en uitvriezing.
Daarom zendt waterdamp uit vanaf ca 5 km, met een zwaartepunt op ca 8km, en CO2 gelijkmatiger over een groter gebied tussen de 8 en 20 km.
> Je zou wellicht kunnen zeggen, de weersverschijnselen drukken de tropopauze omhoog (extreem bij diepe convectie), de van nature warmere stratosfeer naar beneden. Een ander soort ‘ duiveltje van Maxwell’ is dus aan het werk.
Dit snap ik niet goed. Kun je dat uitleggen?
(Een reactie op de adiabaat volgt later)
@ Theo
Het 'duiveltje' is niet meer dan beeldspraak. Het 'kraantje' dat voorkomt dat warmte van de warme stratosfeer naar de koudere troposfeer diffundeert.
@Arthur
Goed, ik geef me voorlopig gewonnen, als je helpt de bijbehorende effecten te verklaren..
Laat ik eerst proberen om in mijn eigen woorden te verklaren waarom er volgens de klassieke meteorologie een adiabaat is waarin geen warmtetransport van warm naar koud plaatsvindt:
Het effect op een pakket lucht dat zich naar een niveau van minder dichtheid verplaatst, en daarbij uitzet, is dat de temperatuur ervan daalt.
Teruggebracht tot moleculair niveau geldt dat blijkbaar ook voor elk molecuul: bij het verplaatsen naar een niveau met lagere dichtheid, daalt de temperatuur, en omgekeerd.
Door het voortdurend bewegen van moleculen is er continu een soort micro-convectie die de adiabaat in stand houdt.
Dit is de stabiele eindtoestand van de molecuulbewegingen: er is dus geen energie-uitwisseling in de vorm van warmtegeleiding.
Een andere uitleg zou kunnen zijn:
Elk molecuul ondervindt bij van de aarde af bewegen een remmende kracht g, en bij naar de aarde toe bewegen een versnellende kracht g. Dit veroorzaakt een afname van de beweeglijkheid van de moleculen met de hoogte. Dat staat gelijk aan een temperatuurdaling.
(Ongetwijfeld zien natuurkundigen geen tegenstrijdigheid tussen beide verklaringen, maar ik moet er nog even goed over nadenken om te snappen dat beide echt dezelfde ALR zouden geven…)
Een zich automatisch instellende stabiele ALR in de atmosfeer, ook zonder convectie, is dus verder het uitgangspunt.
Maar hoe gedraagt die zich?
Voor een atmosfeer die zich gedroeg zoals ik dacht had ik het allemaal zo'n beetje uitgevogeld, maar deze verandering maakt het er niet eenvoudiger op.
De vraag is met name: wat is het gevolg van verstoringen?
De belangrijkste verstoring kennen we: warmtetoevoeging.
Dat gebeurt namelijk bij verzadigde convectie, door condensatie, volgens een bepaalde formule, over een groot deel (metname de onderste 3 km) van de tot dan toe ingestelde droge adiabaat (DALR) rate. Er ontstaat een ander temperatuurverloop, onderin minder steil, de saturated adiabatic lapse rate (SALR)van 6,5 K/km ipv 10K/km.
De ALR is blijkbaar erg gevoelig voor verstoringen.
Maar wat gebeurt er wanneer alleen de tropopauze (continu) verwarmd wordt? Stopt de DALR dan wat lager en krijg je een vlak stuk in het temperatuurverloop? Zet de stratosferische opwarming lager in en blijft de hoek dus scherp? Of warmt de hele DALR op en verschuift hij naar rechts, waardoor de tropopauze op de zelfde hoogte blijft maar de aarde opwarmt??
En wat gebeurt er als er afkoeling optreedt?
Er is over een groot deel van de adiabaat afkoeling door uitstraling van warmte door broeikasgassen. Die zouden net als de condensatiewarmte bij de SALR een effect op de DALR moeten hebben en hem steiler moeten maken. Een grotere temperatuurdaling dan 10K/km dus.
Want hoe kan opwarming wel invloed hebben en afkoeling niet?
Tot slot: er zijn veel temperatuurprofielen waarbij er over een zeer groot bereik een constante temperatuur heerst.
Het koud-antarctische profiel dat Noor gaf heeft de eerste 3 a 4 km zelfs een stijgende temperatuur, vervolgens van 4 tot 9 km even 5 km een normale adiabaat, en daarna van 9 tot maar liefst 28 km hoogte over 19 km een constante temperatuur.
Hoe is dit te verklaren?
@ Theo
Sorry voor de late reactie, andere bezigheden gingen voor.
Ik denk dat je een aantal begrippen door elkaar haalt.
De toestand van de statische atmosfeer is uit te drukken in bijv de temperatuur gradient. Afname van de temperatuur met de hoogte. Heeft niets met adiabatisch oid te maken.
(Environmental Lapse Rate ELR)
De ICAO heeft een gemiddelde standaard atmosfeer "bedacht", waarin de temp met ~2K/1000' (~6,5K/1000m) afneemt tot aan de tropopause. De harde praktijk wijkt hier nogal van af, zeker in de onderste paar kilometer van de atmosfeer.
De dry en wet adiabatic lapse rate (dalr /walr)zijn de temperatuur veranderingen van volumes lucht die stijgen (of dalen) ZONDER uitwisseling van energie met de omgeving.
Zie http://en.wikipedia.org/wiki/Lapse_rateAls zweefvlieger, verkeersvlieger en sinds kort parapenter kan ik stellig verklaren dat convectie oa ontstaat door opwarming van de grond door de zon, waarna de grond door conductie de lucht opwarmt, totdat een bubble is ontstaan die warm genoeg is om te gaan stijgen. Dit gebeurt met de dalr totdat er wolken ontstaan, daarna volgt deze bubble de walr. Dit hangt uiteraard af van de ELR.
@ Arthur Rörsch
Ook excuses voor de trage reactie ;-)
Het BKE is nodig in de stralingsbalans om het verschil te verklaren tussen de "gemiddelde" radiatieve temperatuur van 255K en de actuele van 288K.
Postma geeft een aantal rekenvoorbeelden van de temp. als je alleen naar de verlichtte kant van de aarde kijkt.
Gemiddeld over de halve aarde 303K (na albedo).
Recht onder de zon zelfs 394K (geen albedo).
De temperatuur op aarde kan door opwarmen van oceanen en grond tijdens de daglichtperiode, en weer afgeven van deze warmte tijdens de nacht goed verklaart worden.
Om dit te kwantificeren op dagelijkse basis is moeilijk.
Hoeveel bewolking en waar (boven aarde of zee), hoeveelheid water in de atmosfeer etc. etc. Zoals ik al aangaf is de boekhouding van dit proces niet eenvoudig.
@ Theo augustus 5th, 201123:25at
Ik kon zo gauw geen goede links vinden, maar het meten van de backradiation is ook al omstreden. Kort door de bocht omdat je geen straling meet, maar een temperatuur (spectrum)
Via de SB formule rolt daar dan een hoeveelheid straling uit.
Ik denk dat Postma cs niet de terugstraling ontkennen, maar het opwarmende effect daarvan. (Net energy flux)
Ik vertaal dat naar bijv. een sauna en een bad met water.
Allebei op 80 C, dan kies ik nog wel voor de sauna, maar absoluut niet voor het even warme bad. ;-)
De links:
http://claesjohnson.blogspot.com/2011/08/how-to-f…
http://claesjohnson.blogspot.com/2011/08/how-to-f…
@BenAW
Je links baseren zich allebei op de gedachte:
We see that a pyrgeometer does not measure DLR directly but invents it from the formula
E_in = E_net + E_out,
which is supposed to result from E_net = E_in – E_out expressing a Stefan-Boltzmann law of the form
E_net = sigma Ta^4 – sigma Te^4,
where Ta and Te are the temperatures of atmosphere and Earth surface. But Stefan-Boltzmann's law is not described this way in physics literature, where it instead takes the form
E_net = sigma (Ta^4 – Te^4),
which does not allow extracting DLR as sigma Ta^4.
DLR and backradiation is thus fiction invented from an ad hoc formula without physical reality, which is not described in the physics literature. Nevertheless there are companies selling pyrgeometers at price of 4.000 Euro, but of course selling fiction can also serve as a business idea. But is it legal to sell fiction as science? As science fiction?
Dus volgens de schrijver verschillen de volgende twee formules principieel dermate dat de verkopers van Pyrgeometers oplichters zijn:
E_net = sigma Ta^4 – sigma Te^4
E_net = sigma (Ta^4 – Te^4)
Ik zie geen fout hier, en ik ken toevallig de mensen die hier op een steenworp afstand bijna alle extreem nauwkeurige Pyrgeometers maken voor de top-weerinstituten, en dat zijn de zeer serieuze mensen van Kipp&Zn, een eeuwenoud Delfts bedrijf met een dijk van een reputatie.
Als je me uitlegt waarom die Pyrgeometer onzinnige waardes levert, zal ik je links verder uitzoeken.
Vooralsnog vind ik dat de man zich nogal belachelijk maakt met zijn beweringen.
It's Postma all over again ;-)!
@Theo
Als je even naar de bio van Claes Johnson kijkt denk ik dat je de opmerking over zich belachelijk maken zou kunnen her overwegen. http://www.csc.kth.se/~cgjoh/
Andere manier van kijken naar de Pyrgeometers:
je meet de temperatuur van de atmosfeer boven je, gebruikt de SB formule en komt dan op een hoeveelheid straling.
Impliciet neem je dan aan dat de atmosfeer als een blackbody reageert: alle straling wordt opgenomen, omgezet in warmte, en bij evenwicht ontstaat een uitstraling gerelateerd aan de temperatuur. Nou reageert de atmosfeer niet helemaal als een blackbody. UV kan redelijk ongehinderd passeren, en ook IR kan gedeeltelijk vrij passeren. In ieder geval reden om nog eens na te denken over de werking van een Pyrgeometer imo.
@ Theo
Andere uitleg van Postma:
Een schijf met straal gelijk aan de aarde vangt alle zonnestraling op. Na Albedo geeft 1364*0,7 = 955W/m^2
SB geeft dan 360K. Verdeel dit over de dagzijde van de aarde, NIET de gehele aarde zoals Trenberth doet.
Deze temperatuur komt niet voor , dus de warmte is opgeslagen, meest in de oceanen. Hoogste watertemperatuur in diep water is ergens rond de 300K. Door de draaing van de aarde wordt deze warmte meegenomen naar de nachtzijde en straalt daar uit.
Dat dit gemiddeld over de hele aarde (dag EN nachtzijde) 288K oplevert lijkt me heel aannemelijk. Mocht dit al exact te berekenen zijn, en je komt iets tekort, dan kan je altijd nog de vertraagde afkoeling door "broeikasgassen" er bij halen om de laatste (tienden van) graden te verklaren. Geen 33K zoals nu gebeurt. Dit lijkt mij nu weer belachelijk ;-)
@ BenAW
De opwaartse straling van het oppervlak en de neerwaartse straling uit de atmosfeer wordt niet alleen afgeleid uit de SB formule maar uit de spectroscopie (Planck distributie), waaruit dan de bijdrage van elke golfengte wordt afgeleid. (Van de zwarte stralers over hele spectrum, van waterdamp bij zijn rotatiebanden, van CO2 bij zijn trillingsbanden). Dit lijkt mij Postma cs tot dusver te zijn ontgaan.
Voorts de diepwater temperatuur is zeker geen 300 K. Volgens mijn oceanografic handboek, beneden 1 km, 278 K. Aan het oppervlak in de tropen wordt de 300 K gehaald.
@Arthur Rörsch
Wat Postma imo wil aangeven is dat de huidige temp. op aarde keurig is te verklaren zonder BKE, door de inkomende zonnenergie (1364 W/m^2). Door alleen naar het daglicht deel van de aarde te kijken kom je op veel hogere temperaturen dan de gemiddelde 288K waar iedereen van uitgaat. Het effect van de "broeikasgassen" is dan daadwerkelijk het vertragen van de afkoeling.
Ik bedoelde met diep water aan te geven dat er waarschijnlijkwel wat meertjes oid zijn die nog veel warmer worden dan 300K. De intentie was oppervlakte temperatuur van diepe wateren.
Zie ook een aantal commentaren van Postma hier:
http://climaterealists.com/index.php?id=8119
Bijv. deze:
The internal physics of the system is not something I wanted or needed to focus on. It was much more important to discuss the issue of boundary conditions. My Figure 6 was a summary of the actual boundary conditions that exist, and these are quite different from the standard GHE model. With physically real boundary conditions established, it thus becomes much easier and much more physical to discuss the issues I presented on pp11-12 – that the day-time doesn't actually achieve the temperature of the solar insolation because energy gets absorbed into other degrees of freedom.
@BenAW
Wat Postma op hoofdlijnen beoogt, begrijp ik best en waardeer ik ook. Zijn manuscript heb ik voor publicatie al paragraaf na paragraaf van commentaar voorzien en bediscussieerd met de groep waar hij deel van uitmaakt, "The slayers of the Dragon". Aanvankelijk stuitte mijn commentaar op grote weerstand maar in de daarop volgende weken kreeg ik meer waardering en men begon wel te begrijpen dat men toch wel een aantal klassieke elementen van de broeikastheorie over het hoofd heeft gezien. Het eind van de discussie was dat ik werd uitgenodigd om deel van hun groep te gaan uitmaken. Wat ik beleefd heb geweigerd, omdat we met andere sceptische groepen mijns inziens al veel verder zijn gevorderd om inhoudelijke kritiek op de opvattingen van de AGW protagonisten te kunnen uitoefenen.
@BenAW
Ter nadere toelichting, het basis idee van Postma is in orde, dat je bij in beschouwing nemen van de dag-en-nacht wisseling de plaatselijke en lokale verwachte instraling van de zon mag verdubbelen. Maar hij kan niet kwantificeren wat daarvan het effect voor een mondiaal budget is. Met een paar mensen hebben we dat proberen door te rekeningen. We komen dan toch nog altijd 50 W/2 te kort, tussen tijdens de dag in+uit en de nacht uit om de gemiddelde oppervlakte temperatuur op 15 C te houden. Met andere woorden, tijdens de nacht blijft de uitstraling te hoog om de in+uit straling tijdens de dag te compenseren. Wat er ’s nachts aan uitstraling uitgaat, is behoorlijk gedocumenteerd, maar dit wordt door Postma c.s. als gegeven genegeerd.
@ Arthur Rörsch
Dank voor de nadere toelichting. Goed dat er nog mensen zijn die op een intelligente manier naar het klimaat kijken.
Ik vreesde al dat de warmteboekhouding van de aarde nog nooit goed bijgehouden is, en misschien is het wel onmogelijk om dit volledig te kwantificeren.
Ben benieuwd naar resultaten als die bekend worden, of een grove aanduiding van de methodiek om tot een warmteboekhouding te komen.
Leuke balans van NASA ;-) :http://eosweb.larc.nasa.gov/EDDOCS/images/Erb/components2.gif
@BenAW:
Die balans zou toch echt niet door een beginnend accountant worden onderschreven.
De som van de getallen van de opwaartse pijlen zijn 100% ;-)
Heeft iemand een verklaring voor de nogal plotselinge temperatuursverhoging in De Bilt in 1988?
Gemiddelde temperatuur 1951-1987: 8,7 C
Gemiddelde temperatuur 1991-2010: 10,2 C
Trend 1951-1987: -0,25 K/100y
Trend 1988-2010: +1,73 K/100y
Wat is er in 1987-1988 gebeurd?
Excuus, de bovengenoemde getallen hebben betrekking op de gemiddelden over de eerste 7 maanden van het jaar.
Dit zijn de juiste getallen van de jaargemiddelden:
Gemiddelde temperatuur 1951-1987: 9,2 C
Gemiddelde temperatuur 1991-2010: 10,4 C
Trend 1951-1987: +0,33 K/100y
Trend 1988-2010: +1,14 K/100y
Via WUWT:
New paper from Lindzen and Choi implies that the models are exaggerating climate sensitivity.
On the Observational Determination of Climate Sensitivity and Its Implications http://www-eaps.mit.edu/faculty/lindzen/236-Lindz…
Na vluchtig lezen zie ik sporen van Noor van Andel (rol van de tropen).
@ Boels: dan kloppen die getallen niet met beweringen dat het anderhalve graad zou zijn opgewarmd sinds 1980 (kersenplukken van agw'ers die opwarming willen overdrijven door alleen de eerste 7 maanden te rekenen), en met 1,1 graad temperatuurstijging per eeuw zitten we comfortabel
Dat leek mij nou juist het leuke er aan. Zelfs de NASA lijkt te erkennen dat er geen opwarming meer is ;-)
@BenAW: Je testte ons dus op opmerkzaamheid :-)
@BenAW
We zouden hier op aarde in echte problemen geraken als de som van de ingaande pijlen niet hetzelfde zou zijn als de som van de uitgaande pijlen. De wet van behoud van energie dicteert dat zelfs.
Als de uitgaande pijlen minder dan 100% zouden zijn, zouden we hier niet opwarmen, maar uiteindelijk geheel verdampen.
PS, ik heb hier eerder al gepost onder mijn voornaam, maar zag bij het windmolen verhaal een ander jos verschijnen, vandaar de toevoeging 26.
Het verwarrende in het plaatje: als 100% de aarde weer verlaat dan is er geen sprake van opwarming.
En dat bedoelen de makers natuurlijk niet.
Zou niet durven.
In de beruchte Trenberth stralings"balans"is er wel degelijk een onbalans van 0,9 W/m^2. Neem aan dat die bedoeld is on de opwarming te verkaren. NASA heeft het daar niet meer over.
@Boels
Volgens de AGW theorie moet de aarde juist opwarmen om bij meer CO2 toch evenveel uit te stralen als te absorberen.
De variabele is niet dat evenwicht maar (volgens hen) de oppervlaktetemperatuur.
En (volgens ons) de hoeveelheid warmte die in de watercyclus omgaat.
Working every day by day I’m a lot more impressed by your post. Thanks for your personal efforts with expressing the following theme.