
Mijn recente ‘posting’ over Vahrenholt (‘De koude zon’) heeft veel losgemaakt. Niet alleen een record aantal reacties, maar ook een interessante lezersbrief van Kees Jaspers met uitvoerige verwijzing naar een recente analyse van diens voormalige collega Ton Nillesen.
Kees Jaspers:
Het onderstaande schreef ik aan mijn contactpersonen waarvan ik weet dat ze over enige kennis beschikken om het te begrijpen.
‘De reden van dit schrijven is het voortgezette onderzoek van Henrik Svensmark e.a. over de oorzaak van klimaatschommelingen.
Mogelijk heb je al eens van hem gehoord.
Ik heb indertijd o.a. een boek van Henrik Svensmark gelezen over de invloed van kosmische straling op het klimaat (2007). Hoewel het mij best aannemelijk in de oren klonk waren er geen voldoende harde bewijzen. Het karwei was nog niet af.
Nu blijkt men een heel eind gevorderd te zijn.
Als dit te lastig of onnavolgbaar voor je is, adviseer ik de bijlage te lezen.
Dit boekje is geschreven door mijn voormalige collega Ton Nillesen, net als ik gepensioneerd.
Al een decennium lang verzetten wij ons tegen de valse en te snelle conclusies aangaande klimaatverandering die door het IPCC worden verkondigd. Dit betekent niet dat het klimmaat niet verandert, het tegendeel is waar. Het gaat er echter om welke verklaring de beste is. Ik denk dat deze heel aardig staat samengevat in het boekje van Ton.
Hopelijk blijkt de komende jaren dat het zelfreinigend vermogen van de wetenschap aangaande het klimaat een aanvang begint te nemen in de volledig doorgeschoten en gepolitiseerde klimaatdiscussie.
Behalve dat, gaat het de burger een hoop minder geld kosten en blijft energie voor iedereen betaalbaar.
Met vriendelijke groeten,
Kees Jaspers’
Kees Jaspers en Ton Nillesen zijn beiden gepensioneerde elektrotechnici en zijn dus goed bekend met Fouriertransformaties zoals beschreven in het boekje van Ton.
Ton heeft bij Philips gewerkt aan het onderzoek en de ontwikkeling van algoritmen voor circuits in televisietoepassingen, Kees aan die van TV-studio- en consumentencamera’s, digitale fotocamera’s, LCD’s en heeft over de driedimensionale kleurenleer van LCD een boek geschreven.
Ik pik een aantal fragmenten uit het boekje van Ton Nillesen, getiteld: ‘Over klimaatschommelingen en waarom het toch kouder zal worden.’
Allereerst de conclusie:
Analyse van schommelingen in het klimaat, die aantoonbaar gedurende duizenden jaren aanwezig zijn, leiden tot de conclusie dat ook de recente klimaatveranderingen worden gedomineerd door periodieke schommelingen. Dit leidt tevens tot de voorspelling dat de temperatuur de komende decennia zal dalen tot het niveau van midden negentiende eeuw.
Wat was de aanleiding dat de auteur zich voor deze materie ging interesseren?
Inmiddels heb ik wel geleerd om weinig waarde te hechten aan doemscenario’s die door wetenschappers voorspeld worden. Zo hebben we de ‘Club van Rome’ leren kennen die rond 1970 allerlei narigheden voorspelde veroorzaakt door tekorten aan grondstoffen. Veel natuurlijke hulpbronnen zoals olie, aardgas en metalen zouden opraken.
Overvloed en lage prijzen belemmeren nu echter, 50 jaar later, de introductie van alternatieve energiebronnen.
Daarna kregen we, voor ons gevoel passend bij de slechte zomers van de zeventiger jaren, de voorspellingen dat we aan het begin stonden van een nieuwe ijstijd. …
Daarna kregen we “Das grosse Waldsterben” door zure regen dat een verwoesting zou aanrichten aan de Europese bossen. Het was na de grootste ophef daarover (1985) dat wij, bij uitzondering, op vakantie gingen naar Duitsland in het Beierse Woud. Collega’s, die ook niet zo erg geloofden in het doemscenario, raadden me gekscherend aan om tijdens die vakantie op de achterbumper de volgende tekst te plakken: “Mein Auto fahrt auch ohne Wald”.
Pas in 2003 verklaarde de Duitse wetenschapsminister dat het Waldsterben gestopt was, terwijl er al gedurende 20 jaren geen reden meer was voor zorg.
Vervolgens kregen we het doemdenken over het milieu. Milieu was, in de politiek, een non-issue tot halverwege de jaren 70 van de vorige eeuw.
Opvallend is echter dat de zorgen om het milieu sterk conjunctuurgevoelig waren. Als het even tegen zat verminderde die aandacht.
De tendens van de publicaties over dit onderwerp was vooral dat onze leefomgeving steeds slechter werd. Gelukkig werd echter professor Bjorn Lomborg in 1997 geïntrigeerd door de bekende econoom Julian Simon die uitvoerig stelling nam tegen de theorie van groeiende schaarste en de volgende onderbouwde uitspraak deed:
This is my long-run forecast in brief: The material conditions of life will continue to get better for most people, in most countries, most of the time, indefinitely.
Die zienswijze is erg logisch. Ieder mens wil immers graag een leuk leven hebben in een aangename omgeving en zal daarvoor zijn uiterste best doen indien zijn eerste levensbehoeftes zijn vervuld. Lomborg kreeg ook die overtuiging en besloot onderzoek te doen aan de ‘Real State of the World’. Al spoedig ontdekte hij dat van die negatieve verhalen weinig klopte en schreef daar een optimistisch briljant boek over. Zoals te verwachten kreeg hij een diarree van negatieve reacties over zich heen, echter niet of nauwelijks kritiek over de inhoud. Hij had gelijk en als wetenschapper aangetoond hoe het milieu er voor stond en wat er zou moeten gebeuren.
Tegelijk met de aandacht voor het milieu en daarmee het streven naar duurzame energie kwam de klimaatverandering in beeld, met name de invloed daarop door menselijk handelen veroorzaakt door CO2-uitstoot van fossiele brandstoffen. In mijn beleving groeide die aandacht uit tot een hysterie, vooral toen er plannen geuit werden om honderden miljarden Euro’s en dollars, per jaar, uit te geven aan reductie van die uitstoot. De uiteindelijk aanzet voor dit document kwam mede doordat ik een artikel las waarin voor een nieuw (2017) windmolenpark subsidie gevraagd werd om elektriciteit te leveren tegen een kostprijs per Kwh die een factor vier hoger lag dan de marktprijs. Weggegooid geld aan een oude techniek!
De belangrijkste reden om dit te schrijven kwam echter uit een publicatie van wetenschappers van het Max Planck-Instituut die de temperatuursverhoging van de afgelopen decennia volledig verklaarde uit natuurlijke schommelingen geanalyseerd uit temperatuurmetingen gedurende 300 jaar. De conclusie komt overeen met die van Salomon Kroonenberg in zijn boek over geologie en klimaat:
Wat we ook doen, kouder worden zal het toch.
Mijn kennis en zienswijze over het klimaat was echter inmiddels ook sterk gevormd door het derde boek dat ik aangeschaft had over klimaat e.d.. Dat boek van Henrik Svensmark verklaart de kosmische reis van het zonnestelsel door het melkwegstelsel als oorzaak van de klimaatschommelingen over periodes van miljoenen jaren. Een fascinerend verslag van de ontdekkingen van een klimatoloog in samenwerking met een geoloog. Van alle mogelijke oorzaken van klimaatverandering is de kosmische straling de enige die een duidelijk invloed lijkt te hebben op het klimaat over elke tijdspanne van maanden tot eonen (tijdperken op geologische schaal).
In een technisch, maar ook voor geïnteresseerde leken grotendeels toegankelijk betoog, stelt Nillesen vervolgens de volgende thema’s aan de orde:
- Klimaatgekte
- Energietransitie
- Invloed van zonneactiviteit en kosmos op het weer
- Klimaatschommelingen
- Schommelingen met kortere periodes
- Analyse van West-Europese temperaturen
- Voorspelling van het toekomstige klimaat
- Voorspellingen uit de zonnevlekkencycli
- Betrouwbaarheid van het IPCC
Hierbij heeft de auteur een enorme hoeveelheid literatuur doorgeworsteld en refereert hij aan het werk van vele wetenschappers.
Een van de opvallende grafieken hierbij is die van Horst-Joachim Lüdecke (verbonden aan EIKE).

Horst-Joachim Lüdecke
Nillesen schrijft daarover:
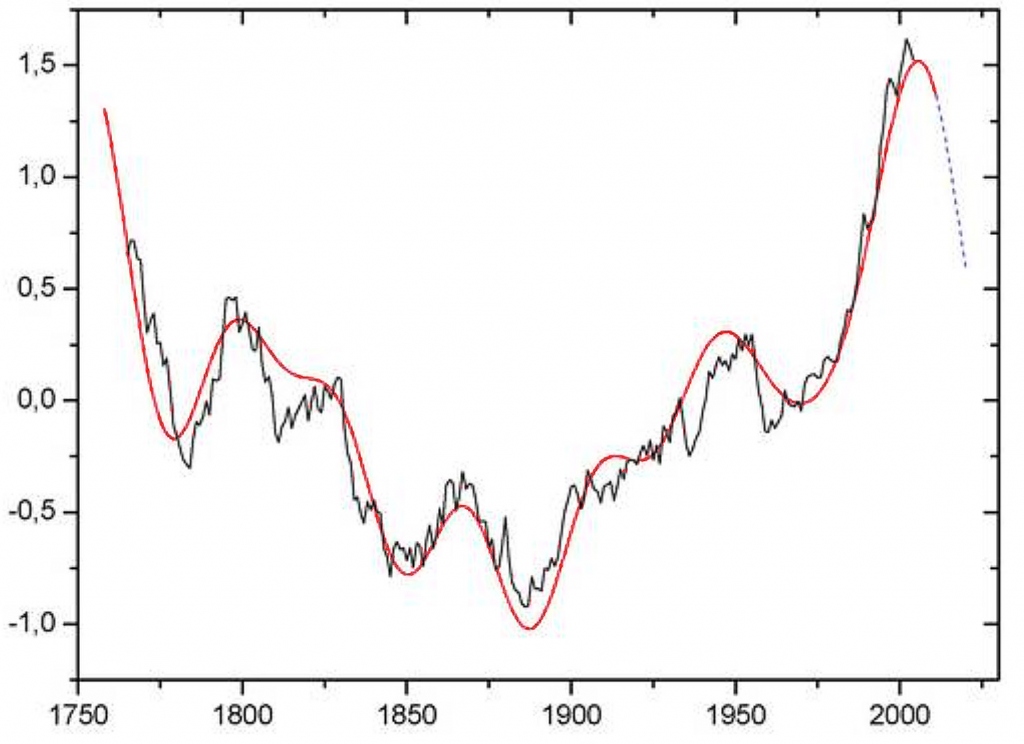
De analyse werd gedaan met een bekende techniek: de “Discrete Fourier Transformatie” (DFT). Dat is een wiskundige techniek om periodieke verschijnselen in gegevensreeksen te ontdekken. … Uit de analyse werden de zes belangrijkste frequentiecomponenten gebruikt, met een periode groter dan 30 jaar, om de volgende reconstructie (rood) te maken van de temperatuurreeks die het gemiddelde was van de zes genoemde meetreeksen (zwart).
Met verbazing heb ik die figuur bekeken, waren de natuurlijke schommelingen zo goed passend bij de huidige werkelijkheid? Lüdecke voegde zelfs een voorspelling toe, de stippellijn met een sterke daling in de nabije toekomst.

Ton Nillesen
Uit de nabeschouwing:
Ik vond het ergerlijk, maar inmiddels vind ik het sneu dat de meerderheid van de journalisten zich achter het vermeende inzicht van politici scharen zonder ook maar een enkele poging te doen om andere ‘waarheden’ voor het voetlicht te brengen. De waarheid is: we weten niet waarom het klimaat is opgewarmd.
Alle voorspellingen berusten op waarschijnlijkheid, geen zekerheid. De verwachting van lagere temperaturen na de analyse van lange- en korte- termijn schommelingen, van eeuwen tot decennia, is echter duidelijk waarschijnlijker dan de scenario’s van het IPCC. De opwinding over zeespiegelstijgingen en broeikasgassen is letterlijk kortzichtig. De ‘alarmerende trends’ zijn natuurlijke variaties ‘met hooguit een toefje mensenwerk erop’.
Aldus Ton Nillesen.
Het volledige boekje is hier toegankelijk.
Aanbevolen voor klimatofielen van alle gezindten.






Wat een wonderlijk mooi verband zien we in de figuur van Horst-Joachim Lüdecke. Ik geloof er geen ene moer van. We zien de overeenkomst tussen het temperatuurverloop van een aantal midden-europese plaatsen en een reconstructie op basis van een ‘Zycklen-Analyse’. Prachtig. Het grappige is dat hij er ook een voorspelling bij geeft. De temperatuurdata lopen tot ongeveer 2002. Is het verder gegaan volgens de voorspelling? Nou, nee. Check maar eens een aantal plaatsen in Midden-Europa. (klik op een plaatsnaam in de onderstaande site)
http://www.logboekweer.nl/International/EuropeTemperatureHistory.htm
Nog niet bijgewerkt voor de laatste paar jaar, maar de boodschap is duidelijk.
@Bart Vreeken,
Eerstens, het door jou genoemde probleem doet niets af aan de bruikbaarheid van de Fourieranalyse.
Verder, zoals bekend wisselt het weer, maar ook het klimaat van plaats tot plaats. Het is dus altijd mogelijk verschillen te vinden. Om dat probleem zoveel mogelijk te ontwijken heeft Lüdecke en Weiss voor een volgende publicatie hogere eisen gesteld aan de datareeks, waarbij lokale afwijkingen zoveel mogelijk (helemaal?) werden gemeden:
“All climate-cycle investigations mentioned relate to local climate. In contrast to these, in the present work [Lüdecke and Weiss 2017], we have investigated dominant cycles in worldwide temperature proxy data of the last 2000 years complemented by instrumental temperature measurements of global temperatures provided by HADCRUT4 [50], from AD 1850 onwards, and by RSS satellite data [51], from AD 1979 onwards.”
Correctie: de temperatuurgegevens van Lüdecke gaan tot en met 2010. De gemiddelden over 15 jaar zijn gecentreerd weergegeven, als ik het goed begrijp. Een correct bijschrift was handig geweest.
Grote waardering voor dit artikel! Hopelijk ben ik nu niet meer de enige die enthousiast is over het toepassen van de Fourieranalyse in de klimaatwetenschap!
Blijft de opmerking van Guido, een aantal weken geleden, dat de rode lijn (voortzetting gevonden sinuslijnen uit het het tijdvak AD 1 tot 2000) van Lüdecke en Weiss zo ongeveer vanaf de eeuwwisseling uit de pas SCHIJNEN te lopen.
CO2 is geen waarschijnlijke reden omdat het dan al veel eerder had moeten afwijken.
Fourieranalyse lijkt mij toch niets anders te zijn dan curve-fitting, zeker als er verder geen theorie achter zit.
De analyse periode gaat zich ook herhalen, dat kan niet anders, wat ook mooi te zien is in het grafiekje van Lüdecke.
Waar komt eigenlijk die hoge temperatuur rond 1750 vandaan, kleine ijstijd, iemand?
Zelf heb ik iets dergelijks uitgehaald met de Hadcrut 4 datareeks, tot in absurdum met hogere frequentiecomponenten. Het lijkt erop dat ik met de komende La Niña goed zit.
Je zal wel iets van de werkelijkheid te pakken hebben, dat het één dag buiten de analyseperiode gelijk 100% fout gaat lijkt niet erg waarschijnlijk.
@Der Ganzumsonst,
“Fourieranalyse lijkt mij toch niets anders te zijn dan curve-fitting, zeker als er verder geen theorie achter zit.”
Je kunt toch moeilijk volhouden dat hier geen theorie achter zit? Die theorie is dat het klimaat een golfkarakter heeft. Na onderzoek met Fourier, maar eigenlijk al lang daarvoor, had men ontdekt dat er naast het dag- en nacht-, zomer- en winterritme en de ijstijdencycli nog veel meer golfpatronen zijn.
En als toetje, het blijkt steeds meer dat van al die (stuk of 10-20, ik heb ze niet geteld) cycli door de zon worden gestuurd!
Dat probleem met de einden bij Fourier behandelt Lüdecke in
https://www.clim-past-discuss.net/11/279/2015/cpd-11-279-2015.pdf
Hoofdstuk 5, rondom de formules 3-4-5. Fragment:
“The parameters of the sine function ν and φ could in principle be taken from the DFT. However, DFT has uncertainty margins and treats the data as infinite recurrences, which is equivalent to compulsory boundary conditions..”
Laat ik het anders zeggen.
Het beschrijven van een signaal m.b.v. de harmonische inhoud van dat signaal is 100% curve-fitting, overtekenen als het ware.
Het bovenstaande als hulpmiddel gebruiken in een zoektocht naar de periodiciteit in de natuur, b.v. ons planetaire stelsel is al van een andere orde.
Echter, hoe vager de opgebouwde theorie, hoe dichter men bij het pure curve-fitten blijft.
@Der Ganzumsonst,
“Echter, hoe vager de opgebouwde theorie, hoe dichter men bij het pure curve-fitten blijft.”
De basisgedachte van de Fourieranalyse is niet zo moeilijk en zeker niet vaag. Ik begrijp daarom niet zo goed wat je met ‘vaag’ bedoelt. Overigens, het is niet ‘puur’, maar wel een zeer goede benadering; in geval van DFT is de Fourierreeks ter plaatse van de discrete punten zelfs helemaal exact.
En dat ‘pure curve-fitting’. Bij de onderhavige toepassing van Fourier is het mooie dat je niet de hele curve hoeft na te lopen, maar in het geval van de laatste Lüdecke 2017, met zegge en schrijven 3 sinuslijnen 2000 jaar temperatuur kunt benaderen met een correlatiecoëfficiënt van 0,84.
Toen ik lang geleden Fourier gebruikte in mijn vakgebied had ik dikwijls aan één golf, de eerste, al genoeg. Dat gaat lekker snel, zeker als je het met alleen de rekenschuif als hulpmiddel moet doen!
Fourieranalyse is wiskunde is gereedschap, nauwkeurig en nuttig gereedschap.
De timmerman (wetenschapper) wrocht uit bouwmateriaal (de data) m.b.v. zijn gereedschap (wiskunde) een huis (theorie).
Met slecht gereedschap bouwt hij een krakkemikkig huis.
Zonder bouwmateriaal geen huis.
Als het gereedschap, de Fourieranalyse, zaligmakend was kun je het zelfs achterwege laten want het resultaat is voorspelbaar.
Neem het begin van de datareeks, brei dat aan het einde en voorspel aldus de toekomst.
Ganzumsonst
Fourier analyse geeft een bevestiging van een periodiciteit die je al op andere gronden vermoedt.
Neem de circa 60 a 70 jarige periodiciteit van de Temperatuur tijd reeks. Je kunt deze onmiddellijk in de grafiek waarnemen, maar het spoort ook goed met een soortgelijke periodiciteit van de AMO, en wordt bovendien ook nog bevestigd met een discrete Fourier transformatie. Dus er zijn meerdere bewijslijnen.
Naast de verzonnen “alarmistische trends” is er een echte waarneembare trend, die echt alarmistsich is.
Je hoeft niet cynisch te zijn om achter de Club van Rome, VN-IPCC, KNMI, milieu- en klimaatwetten, politieke subsidies aan NGO’s en politieke subsidies aan de klimaatwetenschappelijke bubble, het SER+ energie-akkoord, RutteIII extra-klimaat-ambities de 1e wet van Parkinson van toepassing te ontdekken.
1e wet: “Work expands to fill the time available for its completion.”
Het is de onbetamelijke drang van de overheid het ambtelijk pyramidale apparaat, hun hierachieke organisatie, de budgetten en ambtelijke bemoeiienis te kunnen verhogen, (op kosten van de belastingbetaler) zonder de harde doelsteling dat de effectiviteit, beheersbaarheid en betrouwbaarheid van de ambtelijke “productie” en maatschappelik nut toeneemt.
https://nl.m.wikipedia.org/wiki/Wet_van_Parkinson
parasitisme is een volkomen natuurlijk verschijnsel en als overlevingsmodel behoorlijk succesvol.
De geschiedenis is een aaneenschakeling van elites die het volk uitzuigen.
Mijn vertaling van de Trivialiteitswet van Parkinson
De hoeveelheid tijd die in discussies wordt besteed aan een onderwerp is omgekeerd evenredig met de hoeveel kennis die er over dit onderwerp is en/of
omgekeerd evenredig met de belangrijkheid van het onderwerp.
Grappig dat eindelijk duidelijk de naam van Salomon Kroonenberg wordt genoemd. In zijn boek “De menselijke maat” De aarde over 10.000 jaar, laat hij duidelijk de beperkte scope zien van al die alarmisten. Het verbaast me dat de Nederlandse MSM niet volstaan over de warmste jaarwisseling ooit en ook die domme Joep van het Hek onzinnige grappen over het klimaaat maakt. Nee we moeten blijven geloven dat de aarde naar de verdoemenis gaat, terwijl als je het echt in de tijd plaatst (dus tientallen jaren), zich eigenlijk geen rare ontwikkelingen voordoen. Maar door paniek te zaaien, heeft de overheid iets gevonden om haar burgers financieel uit te kleden. En velen trappen in deze leugens.
Het laat allemaal zien dat er nog veel niet of maar zeer ten dele bekend is waar het de klimaatwetenschap betreft. Meer bescheidenheid zou de overheden sieren en bovenal een stuk meer scepsis ten opzichte van het IPCC. Die overtrokken adoratie echter alsmede de hysterische taferelen rond klimaatconferenties en de onophoudelijke propaganda op de kwelbuis verklaren een extreem hardnekkig geval van een, overigens succesvol, georkestreerde nieuwe religie.
Er zijn meer van dergelijke fourier-analyses, want er zijn meer kosmische cycli. De beste toets is en blijft: wat gebeurt er de komende pakweg 30 jaar. December 2017 was overigens verre van de warmste.
Aan de media zouden best eens wat eisen gesteld mogen worden. Zoals de verspreiding van leugens strafbaar stellen. Daaronder valt ook het voor waarheid verkondigen van veronderstellingen. Vergelijk het met oproepen tot een bankrun: dat is ook strafbaar.
Het spijt mij te moeten schrijven dat een interessant onderzoek (Horst-Joachim Lüdecke) op deze wijze om zeep wordt gebracht.
“Wat was de aanleiding dat de auteur zich voor deze materie ging interesseren?”
Wat voegt dat in hemelsnaam toe? En als ik dat dan ook nog ga lezen schiet ik bijna in een stuip.
Erik 2 januari 2018 om 22:53,
Helemaal mee eens, maar dat is niet van toepassing op de Lüdecke-grafiek.
Die vertoont alle kenmerken van het beschrijven van een signaal m.b.v. de harmonische inhoud van dat zelfde signaal.
Beste Ganzumsonst,
Waarom is dit niet van toepassing op de Lüdecke-grafiek?
De belangrijkste sinus in de grafiek is een foutieve (zie hieronder) met een periode van 254 jaar (amplitude: 0,7), maar de 2de belangrijkste en ik zou dus zeggen de echt belangrijke is de 64-jarige sinus (amplitude: 0,28)
Danny,
Omdat nu juist eerste harmonische het beeld van de grafiek bepaald, en daar ook de grootste betekenis aan word gegeven, terwijl het een artefact van de gekozen analysemethode is.
Bovendien, als je de gevonden periodiciteiten niet kunt duiden, blijft het gefröbel.
In het duiden van het resultaat zit de meerwaarde, niet in het toepassen van een stuk gereedschap.
Ganzumsonst,
Toch een wat eigenaardige redenering. De auteurs hebben het over 6 frequenties (met hun amplitudes tussen haakjes): 254 (0,7) – 85 (0.24) – 64 (0.28) – 51 (0.18) – 42 (0.12) – 36 (0.13)
en jij zegt neen, het is enkel de eerste die telt….
En ik heb het al eerder gezegd: het is niet omdat je (nog) geen verklaring hebt voor een bepaald (periodiek) verschijnsel dat dit een voldoende reden is om het verschijnsel te diskwalificeren…
Begin september gaf ik volgende reactie op een grafiek van Eric met Fourier transformatie:
“Zeer interessante plaatjes. Bij het bekijken werd ik even teruggeflitst naar de jaren 80… en de vervelende eigenschap van de Fourier transformatie van een eindig object. Het is nl. zo dat een Fourier transformatie ervan uitgaat dat het signaal oneindig lang is, maw het wordt links en rechts steeds herhaald. Als er dus een significant verschil is tussen de linker- en rechterkant van het signaal zal de FT deze sprong meenemen in zijn uitkomst. Laat dit nu net het geval zijn in de meeste temperatuurreeksen…
Een mogelijke oplossing is dus de trend er eerst uit te halen en pas dan met Fourier aan de slag te gaan en op het einde de trend terug toe te voegen. Dat vermijdt de “artefacten” links en rechts…
…….
PS. Ook Lüdecke & Weiss hadden/hebben? deze eigenschap blijkbaar niet helemaal onder controle”
Mijn opmerking over Lüdecke & Weiss ging in de eerste plaats over de figuur die hierboven in deze blog gebruikt wordt. Het zogezegd voorspellende deel van de grafiek is niets anders dan het herhalen van de linkerkant van de grafiek en heeft generlei waarde.
Laten we even een Woodfortrees equivalent als voorbeeld nemen:
http://www.woodfortrees.org/plot/hadcrut3gl/fourier/low-pass:6/inverse-fourier/plot/hadcrut3gl/mean:12/plot/hadcrut3gl/detrend:0.85/fourier/low-pass:6/inverse-fourier/detrend:-0.85
De rode lijn geeft duidelijk “de vervelende eigenschap” weer.
@ Danny het zou zeer belangrijk zijn te weten wat Lüdecke & Weiss van je opmerking vinden. Vooral omdat dit de intentie van het voorspellen van een koudere toekomst in dit artikel onderuit haalt. Dat beide kanten van signaal op elkaar lijken aan te sluiten is duidelijk.
Frans,
Ik kan mij echt niet voorstellen dat Lüdecke & Weiss zich ondertussen niet bewust zijn dat hun “voorspelling van 2012” nergens op gebaseerd is… In hun 2016 paper zijn ze al heel wat minder uitgesproken, maar wat mij betreft blijft hun extrapolatie nog steeds zeer twijfelachtig… aangezien ze bovendien geen enkele moeite doen om te verklaren waarom de extrapolatie wel degelijk zou mogen gebeuren…
Eén punt is wel duidelijk: het voorspellen van afkoeling op basis van de bewuste grafiek is op niets gebaseerd, en als wij verwachten dat de MSM een sanity check doen vooraleer alarmistische propaganda te verspreiden, dan mogen we op zijn minst ook van climategate verwachten dat ze hetzelfde doen voor de afwijkende meningen…
Danny, ik ben het eens met je analyse over de beperkingen van de Fourier transformatie. Toch geloof ik dat dergelijke ideeën, zoals de onderhavige, door aanname fouten niet terstond naar het grofvuil moeten worden verwezen. De wetenschappelijke methode geeft immers elk idee een kans. Zie de Feynman quote hier boven in de kop.
Mocht het nu inderdaad op termijn kouder worden, dan hebben we natuurlijk inmiddels tenminste drie hypotheses die overeind blijven staan, Naast de onderhavige ook Die kalte Sonne en natuurlijk de broeikas, want daarvoor maakt het niet uit of het kouder of warmer wordt, voor beide is in voorzien.
beste Danny, interessant.
Ik heb foerier ook toegepast op hadcrut3NH unadjusted. Ik heb de last 1560 en 780 samples genomen. Ik ben uitgegaan van een periode van 65 jaar en heb de detrend methode toegepast (bedankt voor de hint). Ik heb de harmonische 2 (1560 samples) en harmonische 1 (780) toegepast.
http://woodfortrees.org/plot/hadcrut3nh/last:1560/detrend:0.888/fourier/low-pass:2/high-pass:2/inverse-fourier/detrend:-0.888/offset:-0.497874/plot/hadcrut3nh/last:1560/mean:12/plot/hadcrut3nh/last:780/detrend:0.79/fourier/low-pass:1/high-pass:1/inverse-fourier/detrend:-0.79/offset:-0.257404/plot/hadcrut3nh/last:780/mean:12
Erik,
OK en hoort hier een bedenking of een vraag bij?
Andre,
Als ik het goed begrepen heb, ben je ingenieur van opleiding. Dus wie beter dan jij weet, dat je een methode enkel binnen zijn grenzen mag gebruiken. Ik wijs er enkel op dat in dit geval de DFT buiten zijn grenzen gebruikt wordt en dus geen enkele waarde meer heeft. Dat betekent overigens niet dat de conclusie die daar eventueel uit getrokken wordt sowieso verkeerd is, het betekent enkel dat de manier om tot de conclusie te komen fout is.
Beste Danny,
Stel nu eens het onwaarschijnlijke theoretische hypothetische geval dat het klimaat grotendeels wordt bepaald door een serie harmonischen. Als je al die harmonischen kent, dan kun je projecteren hoe de serie verder verloopt. Om deze allemaal uit te pluizen heb je een oneindige reeks data nodig. Die zijn er nu even niet. Daardoor kan er geen adequate projectie worden gemaakt. Klaar, helder. Maar door de best mogelijke benadering te verbieden omdat je toevallig even niet een oneindige dataset hebt, verander je niets aan de onjuistheid of juistheid van de oorspronkelijke hypothese/idee dat het klimaat grotendeels wordt bepaald door een serie harmonischen. Als je purist blijft zul je daar dus nooit achter komen want je mag het niet testen. Met een verre van ideale projectie gebaseerd op niet adequate data lukt dat natuurlijk ook niet exact, maar het blijft wel het beste wat je daarvoor hebt en natuurlijk moet je die beperkingen zorgvuldig vermelden.
Ik houd overigens mijn adem niet in.
Wow Andre,
kunnen we even terug naar het begin?
http://www.woodfortrees.org/plot/hadcrut3gl/fourier/low-pass:6/inverse-fourier/plot/hadcrut3gl/mean:12/plot/hadcrut3gl/detrend:0.85/fourier/low-pass:6/inverse-fourier/detrend:-0.85
Welke van de 2 curves – rood of blauw – denk je dat de beste voorspelling voor de toekomst gaat worden?
Beste Danny,
Als je vraagt rood of blauw, dan is dat automatisch de drogreden van het valse dilemma. Misschien is het wel oranje of paars. Ik meen dat de wetenschappelijke methode gaat over het uitsluiten wat het niet is, en niet om te kiezen uit de meest waarschijnlijke. je analyse suggereert -niet onverwacht- dat de hypothese van de serie harmonischen aardig onderweg is naar het ronde archief. Maar daar dan wel in gezelschap van andere populaire verklaringen, zoals de broeikas, hetgeen ik hier in de nodige blogs eerder aannemelijk heb gemaakt. Immers de onjuistheid van een aardig breinspinsel kan niets veranderen aan de status van eerder gefalsificeerde ideeën.
We gaan niet over wat het wel is, maar wel over wat het niet is.
Blauw is niets anders dan een andere manier van gladstrijken, ook in blauw zit geen fysisch model, net als in de rode Fourier-analyse .
Beste Andre,
Je begint je eerste reactie aan mij met: “Danny, ik ben het eens met je analyse over de beperkingen van de Fourier transformatie.” Al hetgeen daarna volgt, doet mij echter vermoeden dat je je toch niet helemaal bewust bent van de draagwijdte van die beperkingen.
Ik heb het eventjes visueel op een grafiekje gezet:
https://www.dropbox.com/s/iay22zqu2vihzjn/H3gl1980.png?dl=0
Als input neem ik HADCRUT3 unadjusted global mean bij Woodfortrees en laat daar de Fourier transformatie op los over een periode van 130 jaar, tot 1980 dus. Eerste maal zonder aanpassing – equivalent aan de figuur in deze blog – en eenmaal na eerst te detrenden (visueel geschat op 0.4). De resultaten daarna overgebracht in een spreadsheet en de signalen geëxtrapoleerd tot 1750 en 2100 resp.
Door slechts de data tot 1980 te gebruiken, kun je dus onmiddellijk een idee krijgen van de voorspellingswaarde van de gebruikte techniek. Ik vermoed dat dit geen commentaar behoeft… en dus enkel bevestigd wat ik eerder schreef.
Over de geëxtrapoleerde stukken van de gedetrende Fourier berekeningen valt wel wat te zeggen: ik heb ook de trend geëxtrapoleerd over de ganse periode: de 0.4 van de inputdata tussen 1850 en 1980 wordt dus iets meer dan 1 over de periode 1750 tot 2100. Het moge duidelijk zijn dat deze techniek misschien enige voorspellingswaarde heeft, maar dan toch nog zeer beperkt en zeker niet langer dan 10 jaar…
Danny,
Je schrijft: ‘… als wij verwachten dat de MSM een sanity check doen vooraleer alarmistische propaganda te verspreiden, dan mogen we op zijn minst ook van climategate verwachten dat ze hetzelfde doen voor de afwijkende meningen …’
Het voordeel van een interactief internetforum als dit blog is dat verschillende gezichtspunten – soms rijpe, soms minder rijpe – aan elkaar kunnen worden getoetst. Hopelijk leren we daar allen van.
“Het voordeel van een interactief internetforum als dit blog is dat verschillende gezichtspunten – soms rijpe, soms minder rijpe – aan elkaar kunnen worden getoetst. Hopelijk leren we daar allen van.”
Als dat zo zou zijn dan zou ik meer terughoudendheid en nuance verwachten in de berichten en op basis daarvan de discussie op inhoud te voeren. Dat zou ik toejuichen.
Mijn perceptie is dat dat niet het geval is en dat het zelflerend vermogen te wensen overlaat gezien het veelvuldig herhalen van minder rijpe ideeën waarbij discussies al snel niet over inhoud gaan maar verplaatst wordt naar 1001 niet rijpe randzaken.
Mijn perceptie heb ik opgedaan door te proberen op inhoud voornoemde minder rijpe ideeën te pareren. Uit weinig is gebleken dat die discussie heeft geleid tot rijpere ideeën. Maar ik blijf hoop houden.
In onderhavig geval ben ik toch zeer benieuwd of de inhoudelijke reacties van Danny in het volgende curvefitting verhaal d.m.v. FT wordt meegenomen.
Marc,
Dank je voor de steun, en hoewel ik heel vaak de indruk heb dat je wel (heel) goedgelovig bent tov de overheid en zijn entiteiten (Tennet om er één bij naam te noemen), ga ik met je akkoord dat een “voortschrijdend inzicht” een absolute meerwaarde zou zijn voor deze site…
Toch even de puntjes op de i zetten en eigenlijk is dit meer bedoeld voor Ganzumsonst dan voor jou, maar aangezien jij zijn woorden overneemt…
Je doet Fourier heel veel oneer aan door zijn transformatie “curve fitting” te noemen. In het geval van temperatuurreeksen transformeer je een tijdssignaal in een frequentiesignaal. En waar in het tijdssignaal een punt heel erg beïnvloed wordt door zijn buren, geldt dit veel minder in het frequentiedomein, de scheiding is zoveel groter in het frequentiedomein en dus ook het daaraan gekoppeld scheidend vermogen.
Het is dus zeer goed mogelijk, enigszins te verwachten eigenlijk, dat je met een beperkt aantal frequentiecomponenten het tijdssignaal aardig kan benaderen. Overigens als je alle frequenties gebruikt, regenereer je ook de ruis en reconstrueer je het tijdssignaal voor de volle 100%, van “fitting” is er absoluut geen sprake.
Danny,
Graag gedaan. Over dat goedgelovige, ik heb veel opdrachten gedaan voor de overheid en mijn ervaring is dat de integriteit van de mensen hoog is. Het stuit mij tegen de borst dat bij voorbaat, zonder deugdelijke argumentatie alles wat van de overheid afkomt wordt neergezet als leugen om de burgers te hersenspoelen. Tegelijkertijd realiseer ik mij ook dat zaken als de beïnvloeding van het WODC een doodzonde is, wat de huidige politiek gelukkig ook vindt, en daarmee niet helpt in het vertrouwen. Echter, ik weiger om op basis van emotie te gaan argumenteren en ben alleen geïnteresseerd in deugdelijke argumentatie waarom welke publieksrechtelijke instelling dan ook het bij het verkeerde eind zou hebben.
Betreft curvefitting, zolang DFT niet als doel heeft om de onderliggende natuurlijke schommelingen te verklaren en te bewijzen, is het wat mij betreft curvefitting. Zonder dat is het niet meer dan een hulpmiddel waar je geen conclusies aan kan verbinden en zeker niet voor toekomstige temperaturen wat met dat plaatje wel gedaan wordt.
Marc,
Ik kan mij niet van de indruk ontdoen dat je toch wel door een erg gekleurde bril kijkt… Zo erg soms dat ik mij afvraag of je eigenlijk nog wel iets kan (door)zien door zo een bril…
Als inwoner van wat vroeger bekend was als de Zuidelijke Nederlanden, heb ik WODC even moeten opzoeken en dus laat ik eventuele commentaar hierop over aan anderen.
Misschien was ik de vorige keer niet duidelijk genoeg: een Fourier transformatie heeft NIETS met curve fitting te maken.
@Danny, wanneer jij van mening bent dat mijn eerste alinea waarbij ik op basis van argumenten i.p.v. emotie stelling neem of de overheid al dan niet integer is, reden is om mij weg te zetten als iemand die het allemaal niet helder ziet dan heb ik de zelfde bedenkingen bij jou. Wat betreft WODC, toenmalig minister Opstelten had zich rechtstreeks bemoeit met de uitkomsten van “onafhankelijke” onderzoeken op het vlak van drugsbeleid. Een doodzonde. Dat is uitgekomen en nu worden de onderzoeken onafhankelijk getoetst in opdracht van het nieuwe kabinet.
T.a.v. het tweede, jij zal ongetwijfeld meer verstand hebben van DFT dus dat wil ik van je aannemen. Het is te lang geleden dat ik mij met DFT bezig gehouden heb dus voorruit, ik zal het geen curvefitting meer noemen.
Variable Chandler and Annual Wobbles in Earth’s Polar Motion During 1900–2015
“The Chandler wobble (CW) and annual wobble (AW) are the two main components of polar motion, which are difficult to separate because of their very close periods. In the light of Fourier dictionary and basis pursuit method, a Fourier basis pursuit (FBP) spectrum is developed, which can reduce spectral smearing and leakage caused by the finite length of the time series. Further, a band-pass filtering method based on FBP spectrum (FBPBPF), which can effectively suppress the edge effect, is proposed in this paper. The simulation test results show that the FBPBPF method can effectively suppress the edge effect caused by spectral smearing and leakage and that its reconstruction accuracy at the boundary is approximately three times higher than the Fourier transform band-pass filtering method, which is based on Hamming windowed FFT spectrum, in extracting quasi-harmonic signals.
..”
https://link.springer.com/article/10.1007/s10712-016-9384-0
@Marc, ik had het over andere replieken van jou, niet deze specifieke waarbij je zegt de ervaring te hebben dat er zeer integere mensen werken bij de overheid. Dat wens ik helemaal niet in vraag te stellen.
Ok begrepen waarom je WODC vermeldde, maar dit is dus een typische reactie, niet alleen weggelegd voor de overheid trouwens: oei wij zijn betrapt… we gaan er iets aan doen (de eerste stap is meestal een commissietje samenroepen)… voilà opgelost… eeuuhhh ja, tot dat weer iemand een ander probleem(pje) ontdekt…
@Boels, inderdaad er zijn zeer vele studies die proberen via allerlei filters de randeffecten van een DFT zo veel mogelijk te beperken; je moet namelijk ook opletten dat je het signaal zelf niet zodanig vervormd/afzwakt dat je het niet langer “ziet”. Als je wat wil experimenteren: de “window” functie in WFT is een simpele filtermethode die de randeffecten elimineert:
http://www.woodfortrees.org/plot/sine:10/plot/sine:10/window
en je kan dan onmiddellijk de gevolgen zien: http://www.woodfortrees.org/plot/sine:10/fourier/magnitude/to:15/plot/sine:10/window/fourier/magnitude/to:15
@Danny en anderen,
Betreffende de ‘einden bij DFT’, zie mijn reactie hierboven, 2 januari 2018 om 11:22. Het gestelde achter de door mij gegeven link en door Lüdecke gebruikte methode zou ik aldus willen vertalen:
DFT met N punten geeft N stuks golflengten met bijbehorende amplituden.
Kies alleen de golven met de grootste amplituden eruit. Het aantal zal afhangen van de gewenste nauwkeurigheid.
Vervolgens ga je een beetje schuiven met de gekozen golven zodanig dat de nauwkeurigheid maximaal is. Bij Lüdecke is dat de grootst mogelijke correlatiecoëfficiënt. Lastig karweitje, maar niet moeilijk om te begrijpen.
Van elke gekozen golf verander je de fase, de golflengte en ook, maar in mindere mate, de amplitude net zolang tot de gewenste nauwkeurigheid is bereikt.
En vertel me nu niet dat dit ongewenste curve fitting is. Al doe je het met Haarlemmer olie of zoiets, als het resultaat is dat je met een paar sinuslijnen een grote nauwkeurigheid kunt bereiken, wat wil je dan nog meer?
beste Guus
Je hebt gelijk, als je met dft een paar golflengten vindt met hoge amplitude, is het vermoeden toch dat je in je extrapolatie dezelfde golflengten mag verwachten. Op die manier wordt de waarde van een extrapolatie beter dan een gefitte curve zonder meer extrapoleren. Al hoewel dat laatste zelfs vaak betere resultaten geeft dan de ipcc modellen.
Temperatuur lijkt meer op een beurskoers: Resultaten behaalt in het verleden geven geen garantie voor de toekomst
@Erik, dat ik gelijk zou hebben, Lüdecke et al komt die eer toe.
Die Fourier analyse met de zes beste golven heeft statistisch geen enkele voorspellende waarde.
Een goede fit “in-sample” over een relatief korte periode met zoveel parameters (zes frequenties, zes amplitudes en zes fases, dus in totaal 18 parameters) zegt niks over de voorspelling “out-of-sample” .
Ik kan dezelfde Fourier analyse doen met bv. de goudprijs en dan zullen de beste zes golven ook een prima fit geven over de laatste decennia, doch daarmee kan je echt de goudprijs niet voorspellen.
Statistisch is dit Lüdecke verhaal dus onzin. Hetzelfde geldt voor de IPCC modellen met te veel parameters en dus een prima fit “in-sample”. Dat zegt niks zegt over de voorspelling “out-of-sample”. Dat blijkt ook uit de out-of-sample IPCC projecties versus de temperatuur waarnemingen vanaf 1998 .
Daarbij komt nog dat de monotoon stijgende CO2 curve amper variatie vertoond en dus empirisch (als verklaarder van de hevig schommelende temperatuur) van geen enkele waarde kan zijn. Statistici noemen dat “multicollineariteit”.
Vanwege die multicollineariteit kan je dus statistisch niet bewijzen dat CO2 invloed heeft op de temperatuur (en ook niet dat het geen invloed heeft). Iedere correlatie met zo’n monotone curve als CO2 betekent daarom niks (laat staan causaliteit).
@Wouter,
Lüdecke bedrijft geen statistiek, maar is vooral op zoek naar cycli.
En ja, dan is een temperatuurreeks van een paar honderd jaar eigenlijk te kort, maar niet helemaal zinloos. Trouwens Lüdecke zegt zelf ook dat voor dit soort onderzoek langere termijnen nodig zijn. En goede documentatie van allerlei cycli is weer van belang om met de zonnecycli te vergelijken en zodoende van groot wetenschappelijk belang.
Ik zou dus woorden als niks dit en niks dat in dit verband niet gauw gebruiken.
Overigens zou ik het Engelse woord ‘predikt’ in deze liever vertalen met ‘verwachten’; onze weersverwachting komt ook niet altijd uit.
Hans Erren en Wouter,
hier een parabolische fit van CO2 mauna loa, tot 1998 en vervolgens totaal. Plus extrapolaties van beide tot 2050.
https://www.dropbox.com/s/855mgeolfvhq0jm/Screen%20Shot%202018-01-04%20at%2010.49.25.png.pdf?dl=0
Ik kan me niet voorstellen dat gevonden cycli in het temperatuur signaal niet zouden doorwerken na de gebruikte periode. Dit omdat deze cycli vaak op natuurlijke wetmatigheden berusten.
https://www.dropbox.com/s/y8h81ty8x1lwyn0/Screenshot%202018-01-04%2011.20.43.png?dl=0
Erik,
Enig idee waarom de atmosferische CO2 zich aan jouw formules zal houden?
Deze curvefit doet in elk geval een poging om e.e.a. te relateren aan natuurlijke verschijnselen.
https://tinyurl.com/the-mauna-loa-CO2-curvefit
ganzumsonst
ik vind hetzelf ook vreemd dat de extrapolatie vanaf 1998 zo goed spoort met die van sedert eind 2017. Zal wel komen door de fraaie monotoon stijgende CO2 curve.
De CO2 uitstoot kan hiervan niet de oorzaak zijn lijkt me.
Toch wel, de CO2-uitstoot is ook monotoon stijgend, vergelijk maar met een koffiefilter, het is gewoon een laagdoorlaatrespons.
Hans, je hebt gelijk. De uitstoot is zelfs minder grillig.
Nog een extrapolatie. Een parabolische trend plus een 60 jarige cyclus zijn in 1980 bepaald.
Daarna geëxtrapoleerd tot heden en vergeleken met de werkelijke data.
https://www.dropbox.com/s/785qj7w0jd98db0/Screenshot%202018-01-04%2011.44.42.png?dl=0.
Dank je wel, Danny. Het punt is duidelijk. Maar voor de goede orde: In je grafiek meen ik te zien dat de extrapolaties gelijkvormig zijn aan het basissignaal Fourier-Lowpass6′. Dat zou je niet verwachten wanneer je de gevonden hoofdharmonischen eerst separaat extrapoleert voor ze bij elkaar op te tellen. Ik dacht dat dat het idee is van de Fourier transformatie.
Maar nogmaals ik houd mijn adem niet in. Ik ben het ermee eens dat de ’trainingsperiode’ veel te kort is. Maar daardoor is de foutmarge te groot en zal de uitkomst uiteraard nooit een definitieve falsificatie kunnen opleveren van de hypothese dat dat het klimaat grotendeels wordt bepaald door een serie harmonischen (waar zeker Judith Curry en haar onzekerheidsmonster niet in geloven).
Andre,
Dank je om mijn vermoeden te bevestigen. Als je schrijft “In je grafiek meen ik te zien dat de extrapolaties gelijkvormig zijn aan het basissignaal Fourier-Lowpass6” kan ik alleen maar antwoorden: ja, inderdaad dat is nu net wat DFT (Discrete Fourier Transform) is: zowel het inputsignaal als de Fourier transformatie worden links en rechts tot in het oneindige herhaald… had ik dat al niet vermeld in mijn allereerste reactie op deze site ;-) …en ook nog eens gequote hierboven (Danny 3 januari 2018 om 16:41 ) ;-) …
“Dat zou je niet verwachten wanneer je de gevonden hoofdharmonischen eerst separaat extrapoleert voor ze bij elkaar op te tellen. Ik dacht dat dat het idee is van de Fourier transformatie.”
Spijtig, maar nee dus.
Of dit noodzakelijkerwijze ook betekent dat de gevonden frequenties echt niet mogen geëxtrapoleerd worden, is een andere discussie: in principe dus nee, maar als je alle frequenties hebt kunnen bepalen die van belang zijn in het venster dat je wil bekijken, dan kan het wel… Het is alleen duidelijk dat een venster 1850-2000 niet voldoende is om Bray, Eddy, De Vries-Süss of zelfs Gleissberg cycli te detecteren (BTW dit is een duidelijk voorbeeld van voortschrijdend inzicht, enkele maanden geleden had ik nog nooit gehoord van deze cycli…) en een juiste plaats toe te kennen… Lüdecke et al. 2012 is dus absoluut fout, Lüdecke et al. 2016 gaat zeker de goede weg op maar is meer dan waarschijnlijk toch nog niet de finale oplossing (ik kom hier waarschijnlijk nog op terug)
Beste Danny, nogmaals dank, ik beken onmiddellijk schuld dat ik je eerdere bijdrages slechts marginaal heb verwerkt. Maar, sheesh, Discrete Fourier Transform, herhaling van het (totale) signaal, daar ben ik nog niet helemaal uit. Wie gaat nu al die natuurlijke cycli vertellen dat ze allemaal gelijktijdig pas op de plaats moeten maken, total exact dezelfde fase verhouding van het begin van het combinatiesignaal zich opnieuw voordoet? Waar vind je zo’n maestro?
Ofwel, als je met zo’n uitgangspunt een hypothese moet verdedigen, dan heb je toch echt jezelf geen schijn van kans gegeven.
Erratum:
Hoe krijg je zoiets voor elkaar? :P
Andre,
Nu stuur je de slinger toch wel heel ver de andere kant op… Zo negatief hoor je nu ook niet te zijn over Fourier. Zoals ik hierboven al aangaf, ben ik Lüdecke & Weiss 2016 een beetje dieper aan het bekijken en hun resultaten op grafiek aan te zetten. Tot hiertoe ziet het er heel veelbelovend uit en dan druk ik mij eigenlijk nog zacht uit. Nog even geduld, het komt eraan…
Beste Danny,
Misschien praten we langs elkaar, heel dichtbij, dat wel, maar toch.
Laat me het proberen uit de leggen met deze gelegenheidsgrafiekjes: i68.tinypic.com/i43a5y.png (voor de veiligheid is de link gedeactiveerd, even copy pasten)
H1-H5 in pastelkleuren zijn de vijf hypothetische hoofdcycli die het klimaatsignaal domineren. De vetblauwe kromme “signaal” is de som ervan, het klimaat.
Stel nu, we zijn in het tijdstip tien en we willen een predictie doen van hoe het verder gaat naar twintig, dan kunnen we een “discrete fourier transformatie” uitvoeren en een identiek signaal van 0-10 extrapoleren op de waarden vanaf tien. Dat levert ons de rode kromme “predictie” op. Als alternatief kunnen we een gewone fourier analyse loslaten op het bekende signaal om parameters (frequentie, amplitude, fase) van de vijf hoofd oscillaties (H1-H5) vast te stellen. Met die waardes kunnen we alle signalen (H1-H5) individueel extrapoleren en daarvan de som nemen. Als we het goed hebben gedaan vinden we het vervolg van de blauwe kromme van tien tot twintig. En dat zou dan wel de hypothetische toekomst zijn, in het onwaarschijnlijke geval dat het klimaat vijf hoofdoscilaties kent.
Nu denk ik dat je die rode lijn gewoon naar het ronde archief kan verwijzen. Immers die voorspelling gaat het nooit worden, terwijl toch het hypothetische uitgangspunt “correct” was.
Andre,
Je mag natuurlijk niet de kar voor de paarden spannen, m.a.w. eerst het signaal daarna de 5 hoofdharmonischen…
Om geen detrending problemen te hebben, hierbij een voorbeeld met de AMO index: de amplitude van de verschillende frequenties:
http://www.woodfortrees.org/plot/esrl-amo/fourier/magnitude/to:20
Zijn we akkoord dat de 5 hoofdcomponenten 1, 2, 3, 16 en 18 zijn?
Dat ziet er dan zo uit:
http://woodfortrees.org/plot/esrl-amo/fourier/low-pass:2/high-pass:2/inverse-fourier/plot/esrl-amo/mean:12/plot/esrl-amo/fourier:780/low-pass:1/high-pass:1/inverse-fourier/plot/esrl-amo/fourier/low-pass:3/high-pass:3/inverse-fourier/plot/esrl-amo/fourier/low-pass:16/high-pass:16/inverse-fourier/plot/esrl-amo/fourier/low-pass:18/high-pass:18/inverse-fourier
Zie je het verschil met jouw H1-H5 en het blauwe signaal?
Ik wil echt niet vervelend doen, maar ik ga hier iets gelijkaardigs zeggen wat ik eerder aan Marc zei: je doet Fourier echt veel oneer aan om niet de moeite te willen nemen om te begrijpen wat een Fourier transformatie is… Om het duidelijk te stellen: het is niet wat je denkt dat ze zou moeten zijn :-(
Danny ik wist niet dat ik zo slecht in uitleggen was. Ja ik heb in veertig jaar meer van de Fourier transformatie vergeten dan dat ik geleerd heb en nee ik probeer zeker niet de kar voor de wagen spannen.
Opnieuw dan, mijn grafiekje. Alles wat ik weet is de blauwe kromme tot tijdstip tien, dat is het klimaat dat ik heb “gemeten”. Ik wil weten wat er van tien tot twintig gaat gebeuren en dat “weet” ik nog niet, geen kar voor de wagen. Nu kan ik de gemeten waarden verder extrapoleren en dat levert de rode lijn op. Maar de werkelijkheid gaat anders worden.
Knip en zap, nu zijn we op punt twintig en de werkelijkheid is de blauwe lijn geworden, gewoon het vervolg van de som van H1 en H5, (wat ik niet weet). De rode lijn, mijn voorspelling zat er dus ontstellend naast en mijn conclusie zou dan ook moeten zijn dat mijn hypothetische “klimaat” niets te maken heeft met willekeurig welke 5 harmonischen. En die conclusie is dan ontstellend fout want dat is het nu net wel.
Hoe had ik een betere voorspelling kunnen maken? Dan had ik op basis van het bekende blauwe signaal van 0-10 een analyse moeten maken uit welke harmonischen het was opgebouwd en op de een of andere manier had ik de indruk dat we dat fourier analyse noemden. Maar goed, als ik daarna de geschatte/gevonden harmonischen nu uiteenrafel (zoals de vijf pastel getinte) en individueel extrapoleer dan zou het resultaat wellicht meer hebben geleken op de blauwe lijn dan de rode.
Helpt dit?
André
kun je de link, i68.tinypic.com/i43a5y.png, nogmaals sturen als actieve link. Ik kan hem niet openen.
Danny, de 5 grootste misschien zo iets duidelijker., 1,2,3,16,18
http://www.woodfortrees.org/plot/esrl-amo/fourier/low-pass:1/high-pass:1/magnitude/to:20/plot/esrl-amo/fourier/low-pass:2/high-pass:2/magnitude/to:20/plot/esrl-amo/fourier/low-pass:3/high-pass:3/magnitude/to:20/plot/esrl-amo/fourier/magnitude/from:4/to:16/plot/esrl-amo/fourier/low-pass:16/high-pass:16/magnitude/from/to:20/plot/esrl-amo/fourier/low-pass:18/high-pass:18/magnitude/from/to:20
Beste Erik
De link werkte net voor mij wel. (maar soms ook niet). Probeer deze maar eens: https://www.dropbox.com/s/057473l9j407ro3/fourier.PNG?dl=0
Erik, Andre,
Soms wel lastig om reacties op te merken als je niet “constant” de website scant terwijl er veel trafiek is…
Inderdaad Erik, dit is misschien nog duidelijker, maar mijn vraag blijft staan “Andre, zie je het verschil met jouw H1-H5 en het blauwe signaal?”
PS. De Lüdecke & Weiss 2016 evaluatie komt eraan, ik vond het echter wel gepast om een bepaalde persoon eerst nog een voor-leesoptie – ik heb geen idee of dit de correcte Nederlandstalige benaming is, een germanist onder de lezers? – te gunnen. Nog even geduld dus…
Beste Danny,
Ik blijf heel erg mijn best doen om echt te communiceren. In mijn betoog is H1+H2+H3+H4+H5 van T=0 tot T=20 overal het blauwe signaal en dus niet een vorm van fourier transformatie. Hier is de excel sheet daarvoor https://www.dropbox.com/s/s563srt8vrdndln/geen%20fourier.xlsx?dl=0
Het punt wat ik probeerde te maken is dat extrapolatie van een gecombineerd signaal (zoals de rode predictie) opgebouwd uit harmonischen totaal zinloos is.
Zoals in een eerdere reactie aangegeven kan een extrapolatie van het resultaat van een Fourier transformatie enkel onder strikte voorwaarden. Je moet nl. alle belangrijke componenten voor de periode waarvoor je een voorspelling wilt maken, gevonden hebben… Dat dit zeker niet het geval was voor de grafiek besproken in deze blog heb ik eerder aangetoond en kan hieronder nog eens bekeken worden onder het bestand “H3gl1980”.
https://www.dropbox.com/sh/axty8v4qq5ie4ve/AABxouxqS9nQO7Rrawvu_QWia?dl=0
En nu ik deze grafiek toch in een spreadsheet had, heb ik me even bezig gehouden met de resultaten van Lüdecke & Weiss 2016. Heb mij van in het begin afgevraagd wat zou dat geven als je dit signaal van 3 sinussen gebruikt om af te trekken van het huidige temperatuursignaal en dan verder te werken met dit restsignaal. Dus allereerst, hoe zien die 3 sinussen van L&W eruit in de periode sinds 1850 uit? Dit kan je vinden in bestand “LW2016_detrend”, de groene golf (merk op dat de nul-waarden van de anomalieën van L&W en HADCRUT3 niet gelijk zijn, dus heb ik een offset van 0,35 moeten toepassen)
Het eerste dat hier opvalt, is dat het L&W 2016 signaal voorijlt op de werkelijke temperatuur. Maar dit is dus het resultaat uit een studie dat ongeveer 2000 jaar omvat en waaruit dus 3 sinussen komen die gelinkt zijn aan de zon (een ongeveer 1000-jarige Eddy, een niet-benoemde in de buurt van 500 jaar, en De Vries-Süess van ongeveer 200 jaar). Als je hier wat over opzoekt, zie je dat er heel wat variatie kan zitten op de specifieke lengte van één zo een cyclus, dus het lijkt mij niet onlogisch om deze groene golf te verschuiven met 1 AMO cyclus van 65 jaar die overigens, zeer goed waarneembaar is in het temperatuursignaal (de 3 pieken). Dat geeft dan de bruine golf.
Voor de volledigheid heb ik op deze figuur ook nog de blauwe trendlijn getrokken die gebruikt wordt om de randeffecten van de Fourier transformatie bij Woodfortrees te minimaliseren.
Tenslotte ben ik dan de resultaten voor de eerste 6 componenten voor de WFT Fourier transformatie tussen 1850 en 1980 gaan combineren met deze “bruine golf”. Dit is terug te vinden in het bestand “Voorspelling LW2016_WFT” Er zijn hierop 2 versies te zien: de lichtblauwe die bij de bruine golf de waarde van de WFT resultaten t.o.v. de trendlijn optelt en de donkerblauwe die hetzelfde doet, maar dan de WFT resultaten t.o.v. de bruine golflijn.
Ik moet dus toegeven dat ik een dergelijk resultaat in de verste verte niet had zien aankomen… dit is bijna te mooi om waar te zijn… (dus misschien is het wel niet waar…). Maar als ik er nu even van uitga dat het toch waar is, dan is de conclusie wel heel verdragend voor het klimaat, de rol van CO2 daarin en het te verwachten temperatuurverloop. Deze grafiek suggereert nl. dat de invloed van CO2 op het temperatuurverloop tot op heden nauwelijks zichtbaar is… We moeten bijna gaan hopen dat de alarmisten toch minstens een beetje gelijk hebben en dat hun voorspelde opwarming – met de nodige vertraging weliswaar – de komende jaren er toch nog gaat voor zorgen dat de op basis van de zonnecycli te verwachten afkoeling zal kunnen vermeden worden……………..
Ik kijk uit naar jullie (onderbouwde) kritiek hierop.