
Een bijdrage van André Bijkerk.
We hebben eerder in Guido’s recente bijdrage een keur gezien van studies die de gevoeligheid van het klimaat voor verdubbeling van CO2 inschatten tussen 1,5 en 2,5 of meer graden (TCR). Deze schattingen zijn gebaseerd op data uit het verleden, modellen, etc. Maar het blijven inschattingen. Nu kan er een tendens bestaan om aan te nemen dat de waarheid ergens in het midden ligt. En hoe meer studies er bij komen hoe sterker dat midden wordt. Maar zo werkt de wetenschap niet. Wetenschap is de toepassing van de wetenschappelijke methode. Vergelijk de uitkomsten met de natuur en wanneer het niet klopt, dan maakt het niet uit hoeveel studies in het midden liggen.
Nu weten we ook uit analyse van het frequentiespectrum dat de basisgevoeligheid van het klimaat ongeveer één graad per verdubbeling is, te laag voor bovengenoemde inschattingen. Daarom is bedacht dat er positieve feedback in het spel moet zijn om de vereiste klimaatgevoeligheid te bereiken. In eerdere bijdragen, de laatste hier, heb ik laten zien dat er methodes zijn om aan de hand van specifiek gedrag van de data serie in te schatten of er positieve feedback dan wel negatieve feedback in het spel is.
Ik zal proberen om het nog een keer uit te leggen. Wanneer het vandaag warmer is dan gisteren en het morgen nog warmer wordt dan vandaag, dan is dat persistent gedrag. Een serie datametingen wordt persistent geacht wanneer het vaker voorkomt dat het morgen nog warmer is, omgekeerd kan natuurlijk ook, als het gisteren kouder was dan vandaag en morgen nog kouder, etc, ook persistent gedrag.
Nu zijn er verschillende redenen waarom een dataserie persistent gedrag vertoont, positieve feedback is daar één van. Feedback is iets dat na-ijlt. Mosterd na de maaltijd. Als er op het vorige tijdstip positieve feedback zit, komt er op een volgend tijdstip een extra duwtje daarvan mee en dat bevordert persistent gedrag. Omgekeerd, wanneer bij negatieve feedback de volgende stap wordt tegengewerkt door de vorige, is de kans groter dat de stap in tegengestelde richting wordt gezet en dus is er sprake van anti-persistentie.
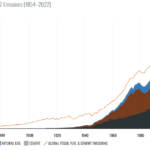
Maar er zijn meerdere oorzaken van persistentie. Er kan een trend zitten in de datareeks, zoals bijvoorbeeld steeds meer verwarming door meer broeikasgas. Factor één dus van Guido’s samenstelling van een datareeks hieronder (met dank aan Guido). Dan is het logischerwijs te verwachten dat het morgen warmer wordt zonder toedoen van enige feedback.
Hoe kun je nu zo’n ruis analyseren? Hiervoor zijn een aantal methodes. Ik heb er twee uitgekozen.
De meest simpele is tellen. Bij elk datapunt kijken we of de volgende stap in dezelfde richting gaat als de vorige stap, omlaag of omhoog. Persistent gedrag. Aan het aantal persistente stappen relatief over het totaal, verwachten we bij positieve feedback meer dan de helft persistentie. Bij minder dan de helft is er dan eerder sprake van negatieve feedback. We zien hier dat de HadCRU4T serie daarmee net onder de 40% komt
Een tweede methode is de vaststelling van de Hurst-exponent bij een trendloze, stationaire dataserie zoals door Olavi Kärner is gedaan. Ik heb dit besproken op dat vorige blog. We zien daar dat enige temperatuurseries rond een Hurst-exponent van 0,4 uitkomen en de conclusie was dat alleen non-persistent gedrag kon worden gevonden op de diverse dataseries. Dit conflicteert uiteraard met de vereiste positieve feedback om de basis-klimaatgevoeligheid van rond de één graden op te ‘boosten’ tot die 1,5 of 2,5 graden of zelfs meer. In de discussie volgend op het blog werden terecht kanttekeningen geplaatst bij de tijdsfactor. Feedback is mosterd na de maaltijd, maar komt dat na een uur of een dag of een maand of een eeuw? En hoe beïnvloedt dat deze twee metingen? Kan een trage feedback onopgemerkt blijven door deze twee methodes en zou daardoor in de werkelijkheid toch positieve feedback mogelijk zijn? Dat gaan we nu bekijken.
Ik heb weer eens een modelletje gemaakt, het JBF-model*, met atmosfeer-achtige data waarbij op een willekeurige data serie (een stationaire random walk) diverse types feedback kunnen worden toegevoegd met diverse tijdsvertragingen om het effect daarvan te bezien op de Hurst-exponent en de persistentietelling. Hier is het “control panel” daarvan in excel:
We bekijken twee gebieden, eerst de energie van de diverse stralingen (licht, infrarood etc.) in abrikooskleur en daarna de daaruit volgende temperaturen in eendei-groen. We beginnen dus in het stralingsgebied met een volstrekt willekeurig maar stationair gemaakte signaal, de random walk in blauw, zonder trend (G3), deze heeft een Hurst-exponent van 0,51 (H3) en een persistentietelling van 50% (I3), vrijwel neutraal dus. Beide hebben een foutmarge (standaarddeviatie) van ca 0,02, waardoor het ondoenlijk wordt om op precies 0,5/50% uit te komen. 0,51/50% is ‘next best’. Alle kleuren in de grafieken corresponderen met elkaar. In de stappen hierna gaan we de veranderingen in dat signaal zien, wanneer we het gaan modificeren.
Eerst komt er een trend overheen (C4), een nabootsing van de veronderstelde stijgende temperaturen door de broeikasgassen. We zien die trend netjes terug in de output. De Hurst-exponent wordt hierdoor niet beïnvloed omdat we bij de berekening die trend gelijk weer wegfilteren om eerder genoemde redenen. Ook blijkt de trend geen invloed te hebben op de – niet stationaire – persistentietelling op het originele signaal. In de volgende rij voegen we positieve feedback (op de forcing) toe. Dit kan in meerdere tijdstappen. De eerste drie (T1, T2, T3, kolom C, D. E) komen terug in die opvolgende stappen, de vierde T4(-15) in de F-kolom komt terug in twaalf verdere stappen. Hiermee kan dus een trage feedback worden gesimuleerd die slechts geleidelijk inwerkt op het systeem. Kolommen G, H, I laten de output zien, de relatieve verandering in trend, Hurst-exponent en persistentietelling, alle drie verhoogd door deze positieve feedback. De stappen herhalen zich in de volgende rij, 6, waarbij de negatieve feedback in het stralingsdomein alle output waarden weer naar beneden bijstelt.
We gaan nu over naar het temperatuursdomein van het eendei-groen door op de verkregen stralingswaarden de Stefan Boltzmann-relatie toe te passen. We willen weten wat de originele trend zou zijn geweest zonder alle modificaties en daarvoor is de blauwe ‘basic temp trend’ op rij 9. Op rij 10 dan komt het resultaat van de feedbacks in het stralingsdomein met de relatieve trend verandering in vaal bordeauxrood. Hierna doen we de positieve en negatieve feedback stappen nog eens over maar nu in het temperatuursdomein. Het uiteindelijk resultaat zien we in rij 12. Het oranje hokje G12 toont nu een trend van 150%. Vertaalt naar klimaatsgevoeligheid betekent dat hier dat de originele één graad per verdubbeling CO2 door de dominantie van positieve feedback zou zijn verhoogd tot 1,5 graad, de algemeen aanvaarde ondergrens van Guido’s klimaatgevoeligheidsstudies. Het probleem hierbij is echter dat zowel de Hurst-exponent (H12) als de persistentietelling (I12) boven de 0,5/50% uitkomt (logisch) terwijl we toch eerder op HadCRUT4 en soortgelijke series een Hurst-exponent en telling van tegen de 0,4/40% hadden gevonden. De velden G-H-I12 hadden daarom iets van 150%, 0,4 en 40% moeten laten zien en dus zijn we er nog niet.
Om te zien of zo’n uitkomst mogelijk is, gaan we onderzoeken wat er gebeurt wanneer we aan de feedback-knoppen gaan draaien. In het vervolg toon ik alleen de vier rijen met feedback omdat anders de blog veel te omvangrijk wordt. Wat is bijvoorbeeld het effect van snelle en trage feedback:
In 1A zien we het effect van snelle positieve feedback. De trend van het signaal wordt meer dan verdubbeld en de persistentie wordt aanzienlijk veel sterker weergegeven in de telling (70%) dan in de Hurst-exponent (0,54). 1B geeft het effect van een trage feedback, waarbij dezelfde factor 0,5 is uitgesmeerd over 15 keer 0,0333. Voor mij was dit een grote verrassing. De trendverhoging is identiek maar de Hurst-exponent reageert veel sterker (0,62 versus 0,54) terwijl juist de persistentietelling nauwelijks in de gaten had wat er gebeurde (52% versus 70%). Iets soortgelijks zien we bij dezelfde negatieve feedback in 1C en 1D. De snelle feedback (1C) wordt door beide goed geregistreerd (0,33/21%) maar de trage versie (1D) is lastiger voor beide. De Hurst-exponent van 0,37 is nog wel uitgesproken maar de persistentietelling van 48% komt niet boven de foutmarge uit.
We kunnen ook bezien wat er gebeurd wanneer we deze resultaten mixen:
2A geeft een snelle positieve feedback en een langzame negatieve feedback die samen ongeveer een neutrale trend geven. De Hurst-exponent zegt nu anti-persistent (0,41) terwijl de persistentie telling fors persistent aangeeft (69%). Omgekeerd in 2B met langzame positieve feedback en snelle negatieve feedback neigt de Hurst-exponent naar neutraal (0,47) terwijl de persistentietelling fors op negatieve feedback uitkomt (23%). Het laat zich aanzien dat deze asymmetrische resultaten kunnen helpen in de bepaling over de tijdsvertragingen van diverse feedbacks in het systeem.
Maar terug naar het klimaat. Hoe kunnen we aan de feedback-knoppen draaien om te zien hoe hoog we de trend kunnen krijgen, terwijl toch de Hurst-exponent en de persistentietelling in het negatieve gebied kunnen houden? 3A toont hier dan een trend van 118% ofwel 1.2 graden Celsius per verdubbeling, wanneer de basisgevoeligheid één graad Celsius is. Maar dit is wel de uiterste (vier-vijf sigma grens). Immers met een Hurst-exponent en persistentietelling score van rond de 0,4/40% voor de meteorologische dataseries die we hebben bezien, toont 3B dat we niet verder komen dan een trend van zo’n 62% (0,6 graad per verdubbeling). En dat is dus mijn inschatting voor de klimaat gevoeligheid voor 2x CO2, zo die al bestaat.
Science is the believe in the ignorance of experts.




Beste Andre,
Mijn complimenten voor de duidelijke manier waarop je deze complexe materie hebt uitgelegd.
Het 7,2Mb grote spreadsheet kan hier op ‘wetransfer’ worden gedownload.
we.tl/PJ9kiHkj22
Dank, Chemical
Andre
Ziet er ingewikkeld uit, ik heb het nog niet geheel te pakken. Moet er wat meer tijd aan besteden. Maar in zijn algemeenheid kun je stellen dat er wel negatieve feedback moet zijn. Want stel dat er positieve feedback zou zijn, dan zou de temperatuur oplopen door CO2 en vervolgens door waterdamp en daardoor weer meer CO2 en daardoor weer meer waterdamp enz enz. Dat zou uit de hand kunnen lopen en is gelukkig nooit gebeurd.
Overigens kun je de klimaatgevoeligheid voor 2xco2 ook simpel schatten met dezelfde Hadcrut4 reeks. In 2010 was de opwarming sinds 1850 circa 0,8 graad en de CO2 toename circa 120 ppm.
Dit geeft dan een klimaat gevoeligheid van 280/120 * 0,8 *0,5 = circa 0,9 graad. De factor 0,5 betekent dat circa de helft vd temperatuur toename door CO2 komt, hetgeen mi veel te hoog is. Maar het ipcc heeft het over minstens de helft. Dus valt mijn aanname daar net binnen.
Ik ben van mening dat CO2 een niet meetbare invloed heeft vanwege de rustige monotone stijging ervan. Afgezien vd seizoenen zie je geen sprongen in de CO2, terwijl je die bij de temperatuur in hoge mate ziet.
Tot slot André lijkt me je bijdrage wel publiciteits waardig. Waarom maak je er geen paper van voor een tijdschrift, natuurlijk peer reviewed anders is jvdh niet tevreden. Ik heb wel slechtere papers, peer reviewed, gelezen.
Erik,
1. de opwarming is meer dan 0.8 C
2. De opwarming is voor veel meer dan 50% antropogeen eerder 100% (ook 100% is minimaal 50%)
En jij blijft graag naar de ruis kijken om vervolgens te claimen dat het signaal niet duidelijk is
Als eenvoudige beta probeer ik iets van de klimaatdiscussie te volgen, maar als ik deze publicatie en bv een bijdrage als https://www.climategate.nl/2018/01/klimaatgevoeligheid/ met de daarop volgende discussies lees, geef ik het ver voor de helft op.
Niettemin heb ik voldoende wetenschappelijk inzicht om één conclusie te kunnen trekken: de klimatologie is GEEN robuuste wetenschap met kant en klare antwoorden. Ik verwacht ook niet dat daar spoedig verandering in zal komen gezien het chaotische karakter van het klimaat, dat vol met zit met terugkoppelingen.
Dit wordt ook uitgedragen door de sceptische wetenschappers (tautologie) op dit blog, wier voornaamste punt is, dat er zoveel onzekerheid en onkekends bestaat, dat elke conclusie op zijn minst voorbarig is.
Ver hierboven zweeft echter het genie JvdHeijden, die alles in een oogopslag doorziet, maar zo moe wordt van die minderbegaafden, dat hij zijn argumentatie voornamelijk beperkt tot: “Zo is het nu eenmaal…”. Zijn inzicht is zo geweldig, dat hij zelfs zeker weet dat er geen tot nog toe onbekende actoren kunnen bestaan. Hebben toch al die filosofen ongelijk, die beweren dat je nooit het niet-bestaan van iets kunt bewijzen.
Ach Janos, verspil je talent niet en trek je terug op je zolderkamer om een spetterende dissertatie te schrijven of een handboek voor klimaatdummies. Het onbegrip voor je superieure inzicht is zo groot, dat je bijdragen hier toch maar als blog-vervuiling gezien worden. Zonde van de tijd, die je beter kunt inzetten voor de mensheid.
(Ja, ik weet het, je kunt weer inhaken op het woord vervuiling. Doe maar niet!)
@ Paul,
“ Niettemin heb ik voldoende wetenschappelijk inzicht om één conclusie te kunnen trekken: de klimatologie is GEEN robuuste wetenschap met kant en klare antwoorden. Ik verwacht ook niet dat daar spoedig verandering in zal komen gezien het chaotische karakter van het klimaat, dat vol met zit met terugkoppelingen. “
Idd de klimaatwetenschap staat nog in kinderschoenen. We weten te weinig en meten nog te kort en onvoldoende om ook maar iets zinnigs te kunnen schrijven over die complexe processen die een klimaatverandering sturen. Wat we wel weten is dat het klimaat op Aarde veranderd is tussen uitersten van een Aarde met veel ijs en een Aarde zonder ijs resulterend in een zeeniveau grofweg een 100 lager bij maximale ijsbezetting en weer grofweg 100 m hoger bij een ijsvrije Aarde. Dit feit van deze variaties toont aan dat bij beschouwing van alle terugkoppelingen resulterend de demping cq de negatieve feedback uiteindelijk steeds is opgetreden.
Zou dat nu anders zijn door onze activiteiten als mens met het uitstoten van het in de natuur ruim voorkomend CO2? Lijkt mij niet echt aannemelijk.
Paul weet het niet zeker en heeft er ook geen inhoudelijke kennis van maar weet wel zeker dat klimaatwetenschap nog onvolwassen is.
Ja ja de logica van de ” sceptici”, ik begrijp het niet dus anderen ook niet
en ik ben geen genie en ken mijn beperkingen, maar dat betekend ook dat ik het niet beter meen te weten dan de echte experts en dat zijn nu eenmaal die genen die hun kennis publiceren in de wetenschappelijke literatuur.
En als er nog onbekende factoren bestaan met een hele groet invloed dan is mijn mening dat die intussen gevonden zouden zijn na 150 jaar wetenschappelijk onderzoek.
https://skepticalscience.com/big-picture.html voor een beetje basis
Klopt helemaal, JvdH, ik wéét het niet zeker. Daarom lees ik ook de link die jij hierboven geeft. Maar tegelijkertijd geef je haarfijn aan, dat je helemaal blindvaart op de door jou verkozen ‘echte’ wetenschappers, zoals je ook in het merendeel van je reacties laat blijken. Dat blindvaren mag natuurlijk voor een leek, maar het lijkt me tamelijk zinloos, dat hier keer op keer te verkondigen, want de grap van deze blog is namelijk dat ze daar juist NIET op blindvaren.
Inderdaad Paul, de grap op dit blog is dat ze alles klakkeloos aannemen als het ABCD is. Als je langer leest dan blijkt dat de meeste compleet tegenstrijdige ideeën in hun hoofd kunnen hebben als het maar betekend dat we niets hoeven te doen.
Als je ze daar op wijst dat onderzoek iets anders uitwijst is de onderzoeker een alarmist, of ligt het aan de toon van mijn commentaar waarbij ik iets voor de 85e keer weerleg.
Beste Erik
Ik vrees dat het even vastbijten wordt, het wordt nog erger. Je hebt volkomen gelijk over de positieve feedback, als je maar zoiets als een echte positieve feedback factor van zo’n 0,1 invoert, zuiver volgens de definitie, dan ontploft het geheel onherroepelijk. Daarom staat “positieve feedback” tussen aanhalingstekens. In plaats daarvan gaat de feedback over de input en niet over het proces. Je voegt bij de volgende stap nog een deel van de vorige stap toe. Dit levert een goed werkende simulatie van persistent gedrag op maar het is inderdaad geen echte positieve feedback en dat is dus ook een verstorend element in de feedback discussie, de definitie kwestie.
Bedenk ook dat dit meer een onderzoek is naar het gedrag van het systeem, hoe het reageert op alle inputs/forcings, Variatie in zongedrag, variatie in oceaanstromingen, global brightening en dimming, etc en dit vertroebelt de analyse hoeveel opwarming aan CO2 kan worden toegeschreven.
Beste Andre,
Zeer terecht in je antwoord op Erik, stel je terecht positieve feedback tussen aanhalingstekens. Positieve feedback in proceskunde bestaat (waarschijnlijk) niet, en als het al tijdelijk bestaat, wordt het onmiddellijk ingehaald door de normale negatieve proces feedbacks. Er is een beroemde uitzondering, namelijk een oscillator, maar dat vereist 180 graden fase draaiing in de feedback met constante voeding voor de aandrijving. Als ik het begrip positieve feedback hoor in de context van klimaat als verklaring voor de klimaatgevoeligheid, haak ik onmiddellijk af.
Je analyse van de Hurst exponent van data reeksen vind ik origineel om een persistent positieve trend te ontdekken in de reeks. Je hebt echter een lange reeks nodig om een verantwoorde berekening te doen van de exponent, met een niet onbelangrijk factor erbij, dat er niet met de data “geknoeid”mag zijn. Homogenisaties van temperatuurdata zijn niet bepaald bevorderlijk. Waarschijnlijk is het ruwe materiaal van de Bilt vanaf het jaar 1700, als dat nog terug gevonden kan worden, of een waarnemingsreeks uit de UK beter geschikt, in plaats van HadCRUT4.
Dit neemt niet weg dat een klimaatgevoeligheid (TCR) van ca 0,6 graden per verdubbeling CO2 voor HadCRUT4 , waarschijnlijk dicht bij de waarheid ligt.
De Labrijnreeks loopt vanaf 1706 en is al een compilatie van waarnemingen uit Delft, Rijnsburg, Haarlem, Halfweg, Utrecht en De Bilt.
http://members.casema.nl/errenwijlens/co2/debiltseries.gif
Wat is dat nou voor raar plaatje, Hans Erren? Wil je nou beweren dat de gemiddelde temperatuur in De Bilt tussen 1850 en 1930 rond de 10 graden lag? Dat is heel anders dan mij bekend is.
http://www.logboekweer.nl/Antiek/Utrecht1851_Temp.pdf
Ik snap niet dat er zo hoog wordt opgegeven van de ruwe gegevens van een paar eeuwen terug. Die werden niet volgens de huidige normen verzameld, en in een lage frequentie (als je geluk hebt drie keer per dag). Je zult altijd moeten homogeniseren om het vergelijkbaar te maken met de recente meetseries.
Heb je de kleine lettertjes onderaan jouw plaatje wel goed gelezen? Mijn plaatje zijn de ruwe Labrijndata, mooier kan ik het ook niet maken. Leen zijn proefschrift eens als je het niet gelooft.
Die kleine lettertjes heb ik er zelf onder getypt, Hans! Of geplakt, dat weet ik niet meer.
De ‘ruwe Labrijndata’ van Utrecht en andere bronnen zijn 365 x 3 metingen per jaar. In jouw figuur staan dus niet de ruwe data, maar een soort van gemiddelden. De eerste vraag is hoe je die drie waarnemingen per dag omrekent naar een etmaalgemiddelde. Neem je simpel het gemiddelde van de drie, of houd je rekening met de dagelijkse gang van de temperatuur. Dat levert iets anders op. Tweede punt is wat je doet met de locatie in Utrecht. Dat was midden in de stad, daar zal zeker stadseffect in zitten. Als het goed is corrigeer je daarvoor al is het moeilijker om te bepalen hoeveel precies. Daarnaast ligt Utrecht wat westelijker dan De Bilt, daar moet je ook wat voor corrigeren.
Het meetpunt in Zwanenburg lag op een geografisch bijzondere locatie: op het contactpunt van het Haarlemmermeer met Het IJ. Twee grote watermassa’s die vooral ’s winters bij smeltend ijs een afkoelende werking gehad zullen hebben. Ook daarvoor moet je corrigeren. Het is dus niet zo dat de ruwe data (of simpelweg het gemiddelde daarvan) beter is dan de gehomogeniseerde versie.
In jouw figuur zie ik na 1850 uitschieters tot boven de 11 graden. Het KNMI komt op 10,6 voor 1868. Het KNMI komt op een jaartemperatuur van 7,3 graden voor 1855. Jij komt op iets van 8,6 graden. Hele grote verschillen.
Is jouw figuur of iets wat daar op lijkt ook in het proefschrift van Labrijn terug te vinden? Kun je daarvan een plaatje laten zien?
Beste P van Toorn
Dank. Mijn spreadsheet bied plaats aan 2048 datapunten, zo krijg je met de “rescaled range” methode van 8-16-32-….-2048 dus 9 Range/SD estimates. Redelijk solide en HadCRUT4 met maandelijkse data vanaf 1850 komt daarbij in de buurt. In het vorige blog heb ik ook 512 datapunten gebruikt om de maandelijkse satellietdata in te passen en ter vergelijking daarvan vroeg- midden- en late segmenten van HadCRU. Wat opviel was dat de vroege serie vrij lage Hurst exponenten opleverde (rond de 0,25) en de laatste een veel hogere (iets van 0,4). Inderdaad is dan de vraag hoe zuiver de koffie is.
We moeten maar eens naar de Labrijn reeks kijken en naar het resultaat van JRA55 ( jra.kishou.go.jp/JRA-55/index_en.html )
Wordt absoluut vervolgd.
André,
misschien kun je ook de central england temperatuur reeks , CET, gebruiken.
Overigens nog een berekening van klimaatgevoeligheid voor 2*CO2.
Broeikasgassen H2O en CO2 zorgen voor 33 graden temperatuur verhoging tov een atmosfeer zonder deze gassen.
Bij verdubbeling hebben we 560 ppm CO2. We houden H2O constant op 20000 ppm.
De CO2 hoeveelheid is dus klein tov het totaal van waterdamp en CO2
Dus 20280 ppm brkasgas heeft 33 graad verhoging gebracht, dus verdubbeling leidt dan tot 20560/20280 * 33 = 1,0138 graad erbij. Nemen weer aan dat CO2 maar voor de helft verantwoordelijk is dan vinden we een gevoeligheid van circa 0,5 graad.
Dus de klimaatgevoeligheid kan varieren tussen 0,5 en 1,0 bij 50 of 100% CO2 bijdrage aan het effect.
Beste Erik, ik snap dat maar het is niet waar, de broeikasgassen hebben er voor gezorgd dat de atmosfeer tot 33 graden boven de “”blackbody-“”temperatuur kon afkoelen -niet opwarmen. Dubbele haakjes omdat er heel, heel veel aan af valt te dingen.
Zie ook: https://www.climategate.nl/2015/08/mijn-kijk-op-de-invloed-van-co2-op-het-klimaat-deel-een-geen-co2/
Ik zal de CET-data eens tevoorschijn halen.
Erik,
Jouw berekening heeft veel overeenkomst met wat ik hieronder heb gedaan, het gaat over de 5de grafiek in de volgende link:
/https://klimaathype.wordpress.com/2015/12/14/over-de-verzadiging-van-het-co2-spectrum
Dit commentaar had ik vorige week gepost op WUWT.
Verder valt over de grafiek nog het volgende op te merken:
Bij het huidige CO2 gehalte is ca. de helft van het absorberend vermogen van CO2 bereikt, er is verzadiging bij ~2% CO2.
Een opmerking over de atmosfeer van Venus, maar dit terzijde:
De forcering door CO2 is dus maximaal ~20℃, de dikte van de atmosfeer veroorzaakt de hoge temperatuur aan het oppervlak.
In de bovenstaande tekst is dit weggevallen:
“This figure (from the site of Hans Erren) shows the calculated values for the relative absorption over the 15 micrometer band for several CO2 optical thicknesses. 300 atm.cm corresponds to 373 ppm in the air column.
The range 5 – 600 atm.cm CO2 shows a logarithmic response. At 20 000 atm.cm saturation is reached.
It is tempting to calculate from this figure a climate response. Wikipedia learns that GHGs enhance global surface temperature by 33 degrees C, CO2 is responsible for 9-26%, i.e. 3-9 degrees C. The response for doubling CO2 is then ~0.3-1.0 degree C, all other things kept equal.”
De CET dataset hier: metoffice.gov.uk/hadobs/hadcet/cetml1659on.dat
verdeeld in twee segmenten van elk 2048 maanden van 1659-1829 en 1847-2017. De maand-temperaturen zijn in absolute graden Celsius. Daarom moet voor elke maand het gemiddelde in beide periodes worden afgetrokken om de persistentie van de jaarlijkse cyclus te verwijderen. Daarmee zijn we op het basisniveau van HadCRU en andere datasets, die eveneens van temperaturen relatief ten opzichte van het gemiddelde uitgaan.
We krijgen dan een persistentietelling van 29,5% resp. 29,8%.
Na een identieke stationaire behandeling van een random walk, die een gemiddelde Hurst exponent schatting van 50% oplevert, (te weten differentiëren en dan een ‘running average’ van 521 maanden aftrekken) komt de eerste CET set op een Hurst exponent van 0,195 en de tweede op 0,204.
Ter vergelijking, wanneer we die stationair makende stappen overslaan komt een feedbackloze random walk op een Hurst exponent van 0,95-1 en de beide CET datasets op 0,648 resp 0,655
Alles wijst dus op een forse negatieve feedback.
Dit gedeelte is enigszins verwarrend:
“Wetenschap is de toepassing van de wetenschappelijke methode. Vergelijk de uitkomsten met de natuur en wanneer het niet klopt, dan maakt het niet uit hoeveel studies in het midden liggen.”
Dit geldt natuurlijk niet alleen voor studies en hun aantal die in het midden liggen, maar dit geldt voor elke studie, of die nu niet wel of niet in het midden ligt. ‘Zolang het niet klopt, klopt het niet’ staat daar eigenlijk. Dat is een waarheid als een koe.
Dan: ”Nu weten we ook uit analyse van het frequentiespectrum dat de basisgevoeligheid van het klimaat ongeveer één graad per verdubbeling is, te laag voor bovengenoemde inschattingen. Daarom is bedacht dat er positieve feedback in het spel moet zijn om de vereiste klimaatgevoeligheid te bereiken.”
Ik wist niet dat de klimatologen met de modellen de uitkomsten van hun modellen kloppend maakten met feedback. Ik neem aan dat er een serieuze reden is om positieve of negatieve feedback in een model in te voeren en niet alleen om een resultaat kloppend te maken.
Feedback is geen mosterd na de maaltijd. Feedback betekent eenvoudig dat er een systeem bestaat waarbinnen resulterende gegevens/processen de inkomende gegevens/processen steeds en voortdurend versterken (of inhiberen in het geval van negatieve feedback). In een klimaatmodel kunnen dat positieve feedback zijn (opwarming -> toename CO2/waterdamp -> opwarming -> toename CO2/waterdamp -> opwarming etc) en/of negatieve feedback zijn (toename sneeuw/ijs -> verhoging albedo -> afkoeling -> toename sneeuw/ijs ->afkoeling). In de biologische cellen kunnen dat de beroemde metabolische cascades zijn waarin er positieve feedback plaatsvindt: trigger (hormoon) -> cyclisch GMP -> fosforylering van second messengers -> cyclisch GMP net zolang totdat er een tegensignaal komt. Dit heeft naar mijn idee niets te maken met ‘persistent gedrag’, want in de meeste biologische systemen (en dus waarschijnlijk ook in het klimaat) is er sprake van amplificatie van de signalen – een toename van resulterende processen/gegevens.
Marleen, wat je schrijft is onjuist: cyclisch GMP (cq cyclisch AMP) zijn zelf second messengers, ze fosforyleren dus niet andere second messengers, en ze stimuleren evenmin hun eigen synthese.
Amplificatie van signalen gebeurt inderdaad in biologische systemen, maar dat is is iets anders dan positieve feedback. Hierbij wordt het eindproduct weer in het systeem teruggevoerd waardoor een versterkings loop ontstaat. Versterken van een geluidsignaal door een geluidsinstallatie is amplificatie, rondzingen is acoustische feedback.
Het feit dat in biologische systemen amplificatie optreedt (ook negatieve feedback overigens) wil natuurlijk niet zeggen dat dat ‘dus waarschijnlijk ook in het klimaat’ het geval is’.
Chemical,
cyclisch GMP wordt inderdaad als een second messenger beschouwd, maar ik denk toch echt dat de amplificatie toe te schrijven is aan een positieve feedback, in elk geval een feedback die in eerste instantie positief is waardoor er amplificatie optreedt die een inhibitie induceert ofwel negatieve feedback.
Marleen,
Misschien kun je voorbeelden noemen van biologische amplificaties die berusten op positieve feedback, ik ken ze zo een-twee-drie niet. Voor versterken van biologisch signaal is positieve feedback helemaal nodig.
Een voorbeeld van een proces waar heel snel amplificatie van een signaal optreedt is de bloedstolling: in rust staat dit proces helemaal uit, het is zinloos en gevaarlijk om dit systeem op de achtergrond stationair te hebben draaien. Maar als de nood aan de man is, moet de bloedstolling direct op topsnelheid werken. Dit is mogelijk doordat de bloedstolling is georganiseerd als een cascade proces waarin inactieve (pro)enzymen elkaar achtereenvolgens activeren. Hierdoor ontstaat een sneeuwbal effect zodat binnen zeer korte tijd voldoende fibrine gegenereerd kan worden om het gat te dichten.
Een fictief voorbeeld om het principe van dit cascade proces te illustreren: stel dat bij beschadiging van een bloedvat 1 inactief pro-enzymmolecuul(I) wordt omgezet in 1 actief enzymmolecuul(I). Het aldus gevormde enzym(I) werkt vervolgens in op x proenzymen (II), wat resulteert in de vorming van x actieve enzym(II) moleculen. Als 1 enzym(II) molecuul per seconde y proenzymen(III) activeert, worden in de volgende seconde x*y enzym(II) moleculen gevormd. Op hun beurt activeren die in de volgende seconde x*y*z pro-enzymmoleculen (III) enzovoort, enzovoort. Kortom, zonder dat er sprake is van positieve feedback treedt een exponentiële versnelling van het proces op. Het door adrenaline-geïnduceerde snelle vrijmaken van glucose uit glycogeen-stores en talloze intracellulaire signaalroutes zijn op hetzelfde principe gebaseerd.
Voorbeelden van negatieve feedback, waarbij het eindproduct zijn eigen aanmaak remt, zijn er wel, maar dat is een verhaal voor een andere keer.
En wat dit allemaal te maken heeft met feedback in het chaotische klimaatsysteem …?
Paul,
Nee niet blindvaren, maar vooral door de opinie van al die “sceptici” te controleren ben ik er van overtuigd geraakt dat de meeste “sceptici” onzin lopen te verkondigen.
Er is inderdaad een kans dat de mainstream er naast zit, maar als dat zo is zal dat aangetoond worden door mainstream wetenschappelijk onderzoek wat je zal lezen in Nature of Science en niet op een vlaag blog wat de gemiddelde onderbouwing is voor een “sceptische”mening
Marleen 4-2-2018 06.47
Wat feedback betreft denk ik ter vergelijking ook steeds aan de stofwisseling van de levende cel waaraan ik 40 jaar (!) geleden werkte en dan in het bijzonder aan het oscillerende a-periodische gedrag omdat de complexiteitstheorie toen sterk van de grond was gekomen.
Toch denk ik dat er een belangrijk verschil met het klimaatsysteem is wat betreft snelheden waarmee de processen zich afspelen. Er zit wel wat in als André spreekt van ‘mosterd na de maaltijd’. De afbraak van glucose tot pyruvaat oscilleert met een snelheid van een tiental minuten. Veroorzaakt door steeds optredende positieve en negatieve feedback in elk van de stappen.
Op zoek naar de negatieve feedback in het klimaatsysteem moeten we die mijns inziens niet zoeken in een lokale luchtkolom op korte termijn waarin waterverdamping koeling van het oppervlak teweeg brengt maar gelijkertijd de damp ook bijdraagt (door IR absorptie) aan de warmte die in de lage troposfeer wordt vastgehouden. Wat terugstraling opwekt. Positieve en negatieve feedback zullen hier steeds tegen elkaar inwerken maar wat is het gevolg daarvan op een mondiale schaal?
Aanvankelijk zocht ik met modelberekeningen de negatieve feedback in de dag-nacht afwisseling (diurnal cycle) waarbij overdag zowel opwarming van de zon als sterke IR uitstraling tegen elkaar inwerken terwijl in de nacht alleen afkoeling optreedt. Doorrekenend aan waarnemingen boven land leidde dit tot een aanwijzing voor een kleine positieve feedback. Maar dat is dus ook een lokale situatie. Op een mondiale schaal spelen de oceanen (70 % van het aardoppervlak) met een honderd maal grotere warmtecapaciteit dan grond een grote rol. En daarmee met zeestromen ook op de uitwisseling van warmte tussen verschillende breedtegraden. Die speelt zich op een veel langere tijdschaal af dan de diurnal cycle. Heeft alles te maken met de seizoenwisseling, iedere drie maanden. Op zelfs de 60ste breedtegraad is het op het noordelijk halfrond behoorlijk warm gedurende de zomer, maar knap koud in de winter. Maar toch ook niet zo warm of koud als men als gevolg van wisselende zoninstraling zou verwachten. Ik reken door aan 12 situaties, op vier breedtegraden 0, 30, 60, 85 NB, en op vier dagen in het jaar, 21 maart, 21 juni, 21 september en 21 december. En kom dan tot de conclusie in aanmerking nemend de warmte-uitwisseling tussen de breedtegraden op elk tijdstip (door zeestromen en lucht circulaties) van grote betekenis is om een mondiaal jaarlijks berekende gemiddelde temperatuur te verklaren.
Aan een berekening van wat een kleine toename van de optische dichtheid van de atmosfeer op een mondiale schaal door CO2 toename kan veroorzaken, ben ik nog niet toegekomen. Maar ik voorzie nihil. Houdt me ten goede, deze visie is tentatief. Ik moet alles nog eens een keer doorrekenen of ik niet een cruciale fout daarin maak. Dit ook toetsend aan wat de mainstream voor conclusies trekt uit de huidige General Circulation Models.
PS
De discussie die op climategate.nl zo langzamerhand tot stand komt onder mensen die onafhankelijk van de main stream nadenken over de oorzaak van het aardse broeikaseffect waardeer ik zeer. (Die over politieke ontwikkelingen dienaangaande minder). Laten we de wetenschappelijke discussie vooral voortzetten, zonder dogmatisch te worden over AGW alarmistische of sceptische concepten. En kritisch blijven op beide visies.
En daarbij opmerkingen als van JvdH 4-2-2018 12.20 naast ons neerleggen dat alleen main stream publicaties die de modieuze tijdschriften zoals Science en Nature weten te bereiken van betekenis zouden zijn om nieuwe inzichten in de oorzaken van klimaatvariabiliteit te ontwikkelen.
Tot dusver heeft JvdH geen enkel eigen inzicht getoond. Hij volhardt in de opvatting dat de meeste sceptici onzin verkondigen, uitsluitend op grond van de verwijzing naar de main stream views die worden gepubliceerd in de modieuze tijdschriften.
Een mijns inziens populistische benadering om meelezers op het blog af te leiden van wat er zich werkelijk in de wetenschappelijke discussie speelt.
Ik hoop dat die meelezers dat zo langzamerhand ook beginnen te begrijpen.
Arthur,
Ik zou je serieuzer nemen als je overduidelijke onzin (Harde Scafetta) zou afwijzen en eens blijk zou geven dat je open staat voor de mening van anderen.
Oh en natuurlijk het feit dat ik je een jaar of 4 geleden nog moest uitleggen wat OHC was geeft ook al geen vertrouwen.
Ook lezen en proberen te begrijpen wat anderen zeggen schijnt wat lastig te zijn.
als er baanbrekend onderzoek zou zijn over het effect van CO2 dan zal dat uiteindelijk te lezen zijn in Science of Nature en zal de onderzoeker een ticket naar Oslo kunnen boeken.
Maar het geeft allemaal niet ik wacht op je wetenschappelijke publicatie in een fatsoenlijk wetenschappelijk tijdschrift !
André, ik ben (net zoals de meeste anderen die hier reageren) geen klimaatwetenschapper, en heb dus niet voldoende achtergrondkennis. Dus ik kan niet ten gronde nagaan of jij gelijk hebt of niet (alhoewel er hier wel anderen zijn die menen dat wel te kunnen doen!). Ik heb de indruk dat alleen Guido een klimaatwetenschapper is en dus met kennis van zaken kan reageren, en hij blijkt het in ieder geval niet met je eens te zijn. Hij geeft ook heldere argumenten over waar jij je fouten maakt.
Maar als wetenschapper kan ik wel vaststellen dat jouw openingsparagraaf complete nonsens is. Het klinkt wel mooi en het zal bij een naieveling misschien wel de indruk scheppen dat jij weet waarover je het hebt, maar een beetje wetenschapper doorziet dat dit gewoon ‘hot air’ is. Het is immers net het omgekeerde: hoe meer degelijke studies er komen die hetzelfde vaststellen, hoe meer er een breed gedragen consensus wordt bekomen. En daardoor worden de schattingen juist steeds betrouwbaarder. Men gaat van ‘inschatting’ (een veronderstelling) naar ‘schatting’ (een waarde met een betrouwbaarheidsinterval). Hoe meer studies er in dezelfde richting bljiken te wijzen, hoe minder inschatting en hoe meer schatting. Misschien dat je nog eens moet nagaan wat er echt wordt bedoeld met “de wetenschappelijke methode” of “schatting” voordat je die uitdrukkingen nog eens gebruikt.
Alhoewel jij geen (klimaat)wetenschapper bent, meen jij toch het beter te weten dan hen. Daarom enkele vragen:
1/ Heb jij jouw visies al eens met echte (professionele) klimaatwetenschappers besproken? Zijn er die het met je eens zijn?
2/ Ik herhaal mijn vraag van enkele dagen geleden (artikel Klimaat op Venus) : “waarom denk je dat jij het beter weet dan die duizenden experten? is het gewoon omdat je zo graag wil geloven wat jij zegt? omdat het in je overtuiging past?” Toen heb je het niet beantwoord. Kun je het nu wel beantwoorden?
Definieer klimaatwetenschapper
Beste Henk dJ
Mijn opening is exact zo onwetenschappelijk als de conclusie van Guido’s bijdrage onlangs, waarop het was geinspireerd: climategate.nl/2018/01/klimaatgevoeligheid/
Waarom ik gelijk heb met Venus? Ik heb die post gemist anders zou ik onmiddellijk hebben geantwoord. Ik ben geen specialist, maar ik versla elke paleontoloog op het gebied van astrofysica en ik daag iedere astrofysicus uit om zich met mij te meten op het gebied van oceanografie, terwijl ik alle oceanografen uitdaag om zich met mij te meten over kennis van paleontologie. Ik bedoel: je vind het antwoord niet in je eigen kleine straatje, je moet het grote verband kunnen vinden. In 2001 viel ik zowat van mijn fiets onderweg naar huis toen ik spontaan bedacht dat de staat van energie van de aarde en Venus best wel eens gelijkwaardig zouden kunnen zijn. De aarde heeft energie in de rotatie, Venus de warmte. Daar heb ik me op vastgebeten en alles wat ik vond klopte als een zwerende vinger.
Maar wie wil daar nu naar luisteren?
Verder nog, op
Nee, bekend met de publicatie: Hundert Autoren Gegen Einstein? Ook al zijn er 100.000 specialisten het met elkaar eens, de waarheid kan conpleet ergens anders liggen, vandaar de laatste quote:
Als je logische conflicten moet oplossen moet je absoluut de drogreden van autoriteit loslaten.
Ik heb van gedachten gewisseld onder meer met Richard Müller, Judith Curry, Steve McIntyre, William Kinninmonth, Bas van Geel, Patrick Michaels, wijlen Bob Carter, wijlen Zbigniew Jaworowski, wijlen Olavi Kärner enz. Het was altijd heel gezellig.
In aanvulling op Venus: De essentie hier is dat Venus door de chaotische zone ging, waarbij de frequentie van precessie (aarde: 21ka) en obliquity (aarde 41ka) elkaar naderden waardoor extreme interferentie ontstond, ten gevolge waarvan de as van de planeet extreme uitslagen kreeg. De vaste binnenkern, die zich als een onafhankelijke gyroscoop gedraagt, deed daaraan niet mee omdat de torsie krachten op de evenaar uitstulping van de mantel werken. Met de mantel en binnenkern draaiend in verschillende richtingen krijg je een gigantische rem, waardoor rotatie energie werd omgezet in warmte. Die warmte brak vervolgens door naar het oppervlakte en veroorzaakte alle verschijnselen die we nu zien, inclusief de verbranding van de atmosfeer.
André, jouw reacties zitten vol met drogredenen en vermijden om antwoorden te geven op de twee vragen die ik je stelde. Je blijft om de hete brij draaien, en dat zegt zeer veel over jou.
Ik leg uit dat je eerste paragraaf onwetenschappelijk is, maar als enige reactie daarop gebruik je een afleidingsmanoeuvre (de ‘red herring’ drogredenering): je begint over Guido. En dan ga je verder over Venus. Heeft niets te maken met bovenstaand artikel van jouw, dus ook weer een ‘red herring’
Daarbij begin je dan als een bronstige gorilla op je borst te kloppen “ik versla elke paleontoloog… Ik daag iedere astrofysicus uit…” het doet me gewoon weer denken aan de uistpraak van Bertrand Russel: “The whole problem with the world is that fools and fanatics are always so certain of themselves, and wiser people so full of doubts.”
En dan komt de “argumentum ad verecundiam” drogreden. Je probeert je te beroepen op Einstein. Maar Einstein zie nooit dat de natuurkunde voor hem het mis had, hij voegde er enkel iets nieuw aan toe. En ja, in de beginjaren waren er ook wetenschappers die het niet eens waren met Einstein, net zoals met AGW in de jaren ‘90. Maar hoe meer studies er beschikbaar kwamen, hoe duidelijker het werd dat Einstein gelijk had. Net zoals het in de afgelopen 20 jaar duidelijker werd dat AGW beter en beter werd in het inschatten van het broeikasteffect.
En dan nog een “Petitio principii” drogreden: je associeert jezelf met een hele waslijst ‘klimaatwetenschappers’, met wie je van gedachten hebt gewisseld. Is het toevallig dat het allemaal personen zijn die in het kleine groepje zitten van AGW-negationisten? Het is altijd eenvoudig om te ‘bewijzen’ dat je gelijk hebt als je enkel verwijst naar gelijkgestemden. Waar heb je ze ontmoet? Op een lobby-groep symposium van negationisten? Maar heb je ook al eens met een klimaatwetenschapper gesproken die de zeer brede consensus aanhangt?
O ja, en ik vroeg je wel: “zijn ze het met je eens”? Maar daar antwoordde je niet op. Je zegt enkel dat je gesprek “gezellig” was. Ik vond het opmerkelijk dat je hier dus niet hebt geschreven dat ze het met je eens waren! Die hele paragraaf van jou is dus ook weer een “red herring” drogargumentatie.
Je antwoordt dus helemaal niet op de twee vragen die ik je stelde. Uit je antwoorden kan ik maar één zaak concluderen: jij maakt heel wat redeneerfouten maar je bent toch overtuigd dat je –ondanks je beperkte kennis van de klimaatwetenschap- het beter weet dan de duizenden experten die een breed gedragen consensus hebben bereikt na jarenlang onderzoek en discussie. Denk gewoon aan Bertrand Russel: jij bent geen “wise man”, jij bent een “fool”.
We zijn nu wel helemaal op het DH0 niveau beland niet?
paulgraham.com/disagree.html
DH0. Name-calling.
This is the lowest form of disagreement, and probably also the most common. We’ve all seen comments like this:
u r a fag!!!!!!!!!!
But it’s important to realize that more articulate name-calling has just as little weight. A comment like
The author is a self-important dilettante.
is really nothing more than a pretentious version of “u r a fag.”
En omdat je me een idioot vind, hoef je niets van deze blog hier serieus te nemen. Maar is de Hurst exponent en de persistency telling van klimaat data daarmee plotseling wel in het positieve feedback gebied terecht gekomen? Kun je daarmee dus wel de klimaatgevoeligheid boven de basiswaarde uittillen? Waarom weerleg je het blog niet.
En weet je waar consensus zoekers zitten: Hier: en.wikipedia.org/wiki/Groupthink
en daarbij hoort natuurlijk:
waarvan je zojuist een prachtig staaltje hebt laten zien. Waarvoor mijn dank.
André, jij probeert mijn reactie te reduceren tot “Name-calling” en “group-think”. Maar ik heb heel expliciet gemotiveerd waar ik fouten zie in jouw redeneringen, en hoe ik dan tot de conclusie kom dat ik je geen “wise man” kan noemen.
En jij blijkt niet het verschil in te zien tussen “groupthink” ( a psychological phenomenon … irrational or dysfunctional decision-making outcome … without critical evaluation”) en een wetenschappelijk onderbouwde consensus.
Maar jij negeert mijn motivaties wel volledig. Omdat je dat doet, beschouw jij mijn conclusie als “name-calling”. Maar ik zie daarin gewoon weer een afleidingsmanoeuvre van jou. Daarmee probeer je gewoon weer de belangrijkste zaken in mijn reactie te negeren. Die zijn “Je antwoordt dus helemaal niet op de twee vragen die ik je stelde….. jij maakt heel wat redeneerfouten maar je bent toch overtuigd dat je –ondanks je beperkte kennis van de klimaatwetenschap- het beter weet dan de duizenden experten”.
Dus, ga je nog antwoorden op die vragen? Of opnieuw een afleidingsmanoeuvre opstarten?
Andre hier ben ik het toch eens met Henk, als je een artikel schrijft moet je wel inhoudelijk repliek geven. Maar Henk: graag wel alléén inhoudelijk reageren.
Okay, nogmaals dan
Ja en ja
Ik kwam er vanmiddag achter dat mijn visie op Venus oud nieuws is. Het was al bedacht. Ik heb de blog daarover vandaag ingeleverd en het is aan de hoofdredacteur om het te plaatsen. Dan kunnen we er inhoudelijk over discussiëren.
Op verder DH0 gezuig ga ik niet in, hoewel ik me vereerd voel lijdend voorwerp te zijn van karaktermoord.
Ik stel vast: één uiterst minimalistisch antwoord en één ontwijking van de vraag.
TBC !
Ik ben blij dat je niet van je fiets gevallen bent, André!
Maar ik zie werkelijk niet hoe rotatie-energie hier verband zou kunnen houden met de warmte in de atmosfeer van Venus of de Aarde.
In extreme gevallen kan de rotatie van hemellichamen, zoals de manen van Jupiter leiden tot warmte en vulkanisme, omdat ze door de getijdenwerking doorlopend gekneed worden. Maar Venus heeft geen maan, en draait juist langzaam om zijn as. En ook voor de Aarde speelt het voor zover ik weet geen grote rol in de warmteproductie.
Een exotische verklaring zou kunnen zijn als de kern van Venus sneller draait dan de mantel en de korst en zo warmte opwekt. Maar nu verzin ik maar wat en geen idee of zoiets kan. Trouwens best een interessante theorie :-)
Beste Bart
Elke stap daar is te onderbouwen, ik heb niets daarvan verzonnen. Ik heb alleen de stukjes van de legpuzzel in elkaar gepast. Een voorbeeld:
nature.com/articles/35081000
Misschien mag ik van Hans het verhaal wel eens bloggen.
Gelukkig ben je niet echt van je fiets gevallen, André!
Maar ik zie werkelijk niet hoe er verband zou kunnen zijn tussen de rotatie-energie van de Aarde en de warme atmosfeer op Venus.
In extreme gevallen kan rotatie-energie van hemellichamen wel leiden tot merkbare warmteproductie. Bijvoorbeeld bij de manen van Jupiter (of Saturnus?), die worden door de getijdenkrachten permanent gekneed, wat leidt tot vulkanisme. Maar Venus heeft geen maan, en op Aarde speelt het effect voor zover ik weet geen grote rol.
Een exotische verklaring zou kunnen zijn dat de kern van Venus nog sneller draait dan de mantel en de korst, en zo warmte produceert. Maar nu verzin ik maar wat, geen idee of zoiets kan. Trouwens wel een interessante gedachte :-)
JvdH 4-2-2018 17.37
Ik zit niet te wachten op jouw waardering. Je hebt overduidelijk nooit begrepen wat de betekenis was van de bijdragen die Harde en Scafetta hebben geleverd aan voortschrijdend inzicht. Vertel ons eventueel nog eens waarom de berekeningen van Harde en Scafetta niet zouden kloppen. Maar dan echt met eigen getoond inzicht waaruit zou kunnen blijken dat ze fouten maken. Niet met verwijzing naar anderen.
Je weet ook niet in te gaan op bovenstaande discussie met Marleen. Waarschijnlijk begrijp je in het geheel niet waar die over gaat.
Je reacties munten uit in ad hominem. En in onvoorwaardelijk geloof in wat de main stream in Nature en Science gepubliceerd weet te krijgen.
Elke volgende reactie van jou op onze inhoudelijke wetenschappelijke discussie denk ik te kunnen afdoen met verwijzing naar je onvoldoende zelf nadenken over de materie. En kennis daarvan. Als niet ter zake doende omdat je niet toont hoe je er redelijkerwijs zelf op zou kunnen in gaan. De botheid van je niet inhoudelijke respons op bovenstaande discussie met Marleen zal duidelijk zijn voor elke meelezer.
Wat Scafetta heeft gedaan is een forrier analyse los laten op de temperatuur en vervolgens daar cycli van hemellichamen op geprojecteerd om vervolgens te concluderen dat de hemenlichamen de temperatuur van de aarde beïnvloeden, wat hij niet heeft gedaan is een mechanisme geven hoe dat zou moeten gebeuren. Betekenis voor het voortschrijdend inzicht…. NUL.
Wat Harde heeft gedaan is een hoop rekenwerk terwijl logisch nadenken heel eenvoudig zou wijzen op de waarheid –> 100% van de stijging van het CO2 niveau is antropogeen. Betekenis voor het voortschrijdend inzicht –> NUL
Het enige waar die 2 hun nut voor het voortschrijdend inzicht hebben bewezen is dat ze inzicht geven wie goedgelovig is en wie nog even zelf nadenkt voordat hij iemand geloofd.
Allemaal zaken die ik je 4 jaar geleden al heb proberen duidelijk te maken, maar waar je iedere keer weer van wegloopt en niet in gaat op de argumenten van anderen.
http://sargasso.nl/kleine-ijstijd-op-komst/
De discussie met Marleen is nmm ook heel duidelijk
Andre postuleert “Daarom is bedacht dat er positieve feedback in het spel moet zijn om de vereiste klimaatgevoeligheid te bereiken”
Dat is natuurlijk onzin, want de positieve feedbacks zijn niet bedacht die zijn het gevolg van de diverse natuurwetten –> het wordt warmer, ijs smelt en er wordt minder licht terug gestraald –> het wordt dus weer warmer –> er smelt meer ijs
En nog eentje het wordt warmer –> warme lucht kan meet waterdamp bevatten –> waterdamp is een broeikas gas –> het wordt nog warmer.
Ik begrijp wel degelijk waar het over gaat –> Andre geloofd Karner en is zeker dat hij gelijk heeft, Guido, Marleen, Henk Dj en ondergetekende hebben meer vertrouwen in de natuurkunde, de natuurkunde kan namelijk wel de opwarming van de afgelopen 120 jaar verklaren en Andre niet.
Ik heb voldoende zelf nagedacht en geconcludeerd dat jij je verbergt achter lappen tekst, je uitgebreide CV en natuurlijk jouw verder niet onderbouwde mening dat 150 jaar wetenschappelijk onderzoek naar klimaat verandering naar de prullenbak verwezen moet worden want er zou een andere verklaring kunnen zijn.
De botheid van mijn toon? Het zou misschien daaruit voort kunnen komen dat jij al 5 jaar weigert kort en duidelijk te antwoorden op vragen en wegloopt uit iedere inhoudelijk discussie.
En ja jouw mening interesseert me wel want jou mening geeft mensen rugdekking om voorlopig geen klimaatbeleid uit te voeren, dat is waarschijnlijk niet zou erg voor jou, want jij bent intussen 85 en het zal jouw tijd wel duren voor mijn neefjes is dat anders.
Hoe zou jij reageren als James Hanssen zou beweren dat 150 jaar biologie de prullenbak in moet omdat hij meent het beter te weten als het gaat om genetica en dat we moeten stoppen met vaccineren? En als de antivax mensen de mening van James Hanssen zouden gebruiken om te gaan lobbyen om de vaccinatie plicht af te schaffen?
Oh en graag even aangeven waar ik een ad hominem gebruik want conculderen dan de meeste “sceptici”niet nadenken is niet ad hom maar gewoon een feit
Andre, kun je nog een getallenvoorbeeld geven hoe een trage component (lineaire trend) invloed heeft op de hurst exponent, volgens mij filter je die juist weg en kijk je alleen naar de hoge frequenties.
André, Guido,
Toch nog maar eens een kijk op het totale plaatje… met een alternatieve berekening van de klimaatgevoeligheid.
In navolging van mijn eerdere reactie(s) vroeg ik mij af naar wat zijn wij nu eigenlijk op zoek: is er een positieve feedback van de CO2 stijging aan te tonen, rekening houdend met het feit dat het totale systeem tegengekoppeld is, maw negatieve feedback vertoond.
Laten we dus even naar het zuidelijk halfrond kijken: de CO2 evolutie op Mauna Loa en de temperatuur volgens HadCrut4_SH. Uiteindelijk ziet het er zo uit (pag.3!):
https://www.dropbox.com/s/k89e6f9f5to3y08/Temp%20and%20CO2.ppt?dl=0
3 curves, geschaald zodanig dat ze gemakkelijk vergelijkbaar worden:
Blauw/Rood de temperatuur zoveel mogelijk ontdaan van “ruis”: 6-maands gemiddelde lijkt wel bruikbaar…
Het verschil tussen blauw en rood is enkel een detrending van 0.4 °C.
Groen is de CO2 metingen op Mauna Loa geschaald om te passen over de blauwe temperatuurcurve.
Als ik de persistentieberekening juist begrepen heb, vertoond de rode curve een persistentie van 50.85% (120 meetpunten, eerste 2 tellen niet mee, 60 persistente en 58 niet-persistente punten). Voor de blauwe curve geldt dit overigens ook. Lijkt dus wel erg op een “random walk”… is het natuurlijk niet, de grootte van elke “stap” is verschillend van de vorige.
De persistentie van de CO2-curve is wel heel uitgesproken: 82,8% persistent en als je er de trend uithaalt zelfs 83% persistent.
Kunnen jullie hier enige conclusie uit trekken?
Door op deze manier naar de data te kijken, had ik wel zo iets van… waar gaat het nu over: ik zie een “kleine” jaarlijkse variatie in het CO2 signaal, maar een veel grotere variatie in het temperatuursignaal; hoe moet ik nu bewijzen dat er een positieve feedback is van het CO2 signaal in dit veel grotere temperatuursignaal…
Fourier misschien? Laten we daar even naar kijken… Voor het CO2 niveau op Mauna Loa is het redelijk simpel. De 59ste harmonische springt eruit (nota: we hebben vandaag de gegevens voor 59 jaar en 11 maanden, dus 59 is de te volgen weg). We doen dus hetzelfde voor HADCRUT4_SH (van 1959 tot eind 2017)
(zelfde link) pag. 5
Opmerkelijk hoe goed de fases van beide signalen overeenkomen: de temperatuur volgt de CO2 met een vertraging van één maand. Woodfortrees gebruikt de data van Mauna Loa zoals aangegeven als de gemiddelde waarde op de 15de van de maand, maar voor de temperatuur gebruikt men de 1e van de maand, dus 15 dagen extra verschuiving lijkt gepast, vandaar mijn omschrijving van 1 maand vertraging…
De schaalfactor is zodanig aangepast dat beide sinussen eenzelfde amplitude hebben en dit wordt dus mogelijk door een schaalfactor van 0.00461 toe te passen, wat overeenkomt met een klimaatgevoeligheid van 1.146 °C bij een CO2 verdubbeling.
Maar om de dingen ook even in perspectief te plaatsen: in de temperatuuranalyse is de 59e harmonische “minder belangrijk”.
(zelfde link) pag. 4
laat de 5 belangrijkste harmonischen van het temperatuursignaal zien en ook de 59e.
Om te besluiten: Mijn oorspronkelijke bedenking van de vorige keer: kan de Hurst exponent onderliggende positieve feedback detecteren in een tegengekoppeld systeem en hoe dient dit dan te gebeuren, wordt door deze blog niet opgelost en blijft dus openstaan.
Beste Danny
Dit is een probleem:
Als je de ruis op persistentie wilt beoordelen, want dat is de essentie, dan moet je die ruis niet eerst wegfilteren. Wat je wel moet wegfilteren is het signaal zelf, met name jaarlijkse cyclus want die veroorzaakt eveneens persistentie wleke niets met feedback te maken heeft.
Maar kijk nog eens goed naar 3A hierboven, een combinatie van een langzame zeer geleidelijk positieve feedback met een snelle forse negatieve feedback levert een “split” op met een lage persistentietelling en een hoge Hurst exponent. Maar in de praktijk hebben alle signalen beide op ongeveer gelijke waarden.
Ik vraag me verder af hoe valide een jaarlijke temperatuurs- en CO2 cyclus direct te koppelen zijn. De gemiddelde temperatuur op Aarde varieert met de hoeveelheid oceaan die de zon ziet. In de zomer van het zuidelijk halfrond ziet de zon veel meer oceaan dan in de zomer van het noordelijk halfrond. Het zonlicht dat geabsorbeerd wordt in de oceanen doet vrijwel niet mee aan de opwarming van het oppervlak. Daarom is de totale aarde warmer in zomer van het noordelijk halfrond en daar heb je dus een temperatuurscyclus die niets met CO2 te maken heeft.
gamehobbies.nl/Wetenschap—Natuur/natuur/1002056795.html
André,
De snelheid van jouw reactie geeft aan dat je mijn opmerkingen helemaal niet serieus neemt, je wil zo snel mogelijk – meestal foutief – tegengas geven.
Ik ga het dus kort houden…
Als je zegt “Als je de ruis op persistentie wilt beoordelen, want dat is de essentie” dan heb ik toch serieuze vragen… de Hurst exponent is ontwikkeld naar aanleiding van het jaarlijkse peil van de Nijl, dat is signaal, GEEN ruis, ik heb geen idee waarom je denkt dat het om de ruis gaat…
Met tegenzin heb ik jouw Excel-file gedownload. Een van de eerste vraagtekens die ik had, is de totaal verschillende manier om positieve en negatieve feedback te berekenen. Ik ga dan onmiddellijk voor een “sanity check”: is het resultaat van positief + negatief gelijk aan negatief + positief, en tot mijn grote spijt moet ik melden: NEEN het is verschillend, maw er klopt iets niet met jouw berekeningen…
Wat jouw opmerking over 3A betreft, dit is toch een grapje hoop ik… ik zie een positieve feedback van 0.675 en een negatieve feedback van 0.5, volgens mijn definitie is dit dus een meegekoppeld en GEEN tegengekoppeld systeem.
Ik nodig je uit om hierop ten gronde te reageren; als je dit niet doet/wenst te doen, is dit de laatste reactie van mij aan jou.
PS. Laat er geen twijfel over bestaan, ik hoop echt dat je een ten gronde discussie wilt aangaan, zodat ook ik nog wat kan bijleren.
Danny ik meen toch echt enige malen te hebben verteld dat positieve feedback over het systeem niet werkt, dan ontploft de zaak onherroeppelijk. Wat wel kan is positieve feedback over de input, waarmee je persistentie heel goed kunt simuleren. Daarom zien we normale negatieve feedback over het signaal en positieve feedback over de input. Maar ik vind het jammer dat je over alle vragen die je vindt meteen een oordeel klaar hebt en een stuk agressiviteit tentoonstelt en daarom juich ik het toe dat je verder je mond belooft te houden.
Verder nog, de Hurst exponent is inderdaad niet ontwikkeld om feedback te onderzoeken. Die uitbreiding is bedacht door Olavi Kärner, waarbij stationaire data moet worden gebruikt.
http://www.aai.ee/~olavi/
aai.ee/~olavi/cejpokfin.pdf
aai.ee/~olavi/2001JD002024u.pdf
en nog een paar. Ik borduur daar alleen maar op voort.
Daarnaast, met mijn spreadsheet kun nu zelf heel goed experimenteren met meekoppeling en tegenkoppeling.
Het laat zich aanzien dat we in cirkels blijven ronddraaien. In die zin dat commentaren gewoon niet worden verwerkt en oude veronderstelling gewoon worden herhaald zoals het negeren van een jaarlijkse temperatuurcyclus ten gevolge van oceaan-continent verschil in het noordelijke en zuidelijke halfrond.
Ik ga verder met mijn spreadsheet. Na een stevige evaluatie meen ik dat het tweede deel, feedback over de temperaturen redundant/overtollig is, omdat dat ook weerslag heeft op de radiatieve balans. Het eendenei-groen moet er dus vanaf. Ik experimenteer nu met multiple runs op positieve feedback die een zeer grote spreiding blijkt te hebben (onstabiel) in de geest dat de standaard deviatie zeer hoog is.
Verder speel ik met de Hurst exponent/persistentie telling ratio (H/P ratio). Deze is bijvoorbeeld 1,33 +/- 0,083 over 25 runs bij een “positieve feedback” van 0,015 over 15 datapunten tegen een negatieve feedback van 0,5 op het eerste datapunt. Terwijl de feedback van alleen het netto verschil (-0,275) over 25 runs een H/P ratio geeft van 1,10 +/- 0,05. Dat zit aardig ver van elkaar uit de buurt om de zwakke positieve op te merken.
Maar we kunnen dat ook “blind” testen, waarom levert iemand me niet een aantal random walk dataseries aan met verschillende “positieve feedback” over de inputs en negatieve feedback over het systeem en ik zal proberen de combinatie van feedbacks zo goed mogelijk in te schatten.
Het gaat dan om kolom J van Jan vanaf rij 10 in het tabblad “cruncher” in we.tl/PJ9kiHkj22
Beste Guido, ik begrijp het niet. Ik meen dat je veronderstelde dat de 33% persistentie van de ruis een neutrale feedback zou zijn. Daarop heb ik indertijd gereageerd met:
en ik geloof niet dat jij daarop verder bent ingegaan. Maar de essentie is: ruis heeft negatieve feedback en een random walk niet. Dan, Als je verschil ziet in de verdelingsdiagrammen. Het is maar net hoe je de random data laat produceren. Naast de basis random generator heb ik gespeeld met de eenheidsstap en een normaal verdeelde random stap die geldt voor de basis brownse beweging. De verschillen in output over het systeem bleken verwaarloosbaar, waardoor ik heb gekozen voor normale random om de rekentijd en omvang van het excel beheersbaar te houden..
André,
Mijn vorige reactie aan Guido waarbij ik de Hurst component gebuisd heb, verdient misschien wel een tweede zit…
Ik heb een aantal curves voorbereid, in overeenstemming met mijn vorige commentaren/kritieken.
Zoals ik op eerder opmerkte, ga je nooit een positieve feedback vinden als de x-as de tijd is… ik heb dus op hint van Guido het CCSM4 model laten lopen op de KNMI Climate Explorer voor RCP8.5 en ook het RCP8.5 scenario gedownload. Daarna heb ik een aantal curves voorbereid met op de x-as de CO2 concentratie en op de y-as de geprojecteerde temperatuur. Ik wil ze je graag bezorgen. Via climategate veronderstel ik dat je mijn E-mailadres kent, gelieve mij dus een mailtje te sturen en ook aan te geven of .ods formaat ok is of je .xls prefereert..
Danny
Ik heb je email adres niet, maar mijn email adres is voornaam en achternaam aan elkaar zonder accent aigu bij gmail.
XLS geniet de voorkeur.