De zon verklaart 93% variantie zeewateroppervlaktetemperatuur t/m jaren ’80; verzwakking ozonlaag zorgde vanaf jaren ’90 voor meer zonnestraling op aardoppervlak waardoor schijnverband tussen CO2 en temperatuur stand hield; vervolgens zorgde de zon in de 21ste eeuw voor verdere opwarming.
Een bijdrage van Martijn van Mensvoort.
Anno 2020 omschrijft KNMI-onderzoeker Geert Jan van Oldenborgh de sterke statistische correlatie tussen de temperatuur en CO2 als “een bijna perfect verband”1. Echter, de relatie tussen zon en klimaat is hierbij als onbegrepen verondersteld2,3.
Dit artikel beschrijft op basis van in totaal 40 jaren rond de zonneminima tijdens afgelopen 130 jaar dat de correlatie tussen CO2 en temperatuur berust op een spurieus schijnverband dat ontstaat uit 2 factoren, namelijk: een geleidelijke toename van de totale zonnestraling + een toename van de hoeveelheid zonnestraling die het aardoppervlak heeft bereikt t.g.v. verzwakking van de ozonlaag.
De variantie in de zeewateroppervlaktetemperatuur [HadSST34] t/m de jaren ’80 wordt voor 93% verklaard door de totale zonnestraling [LISIRD TSI5]; hierbij is wel gebruik gemaakt van een correctie gericht op de jaren rond de secundaire minima. De 22-jarige zonnecyclus levert de natuurkundige basis voor deze correctie want de secundaire minima ontstaan tijdens de fase waarbij de magnetische polen van de zon van positie zijn gewisseld; de primaire minima ontstaan daarentegen tijdens de fase met de polen in de oorspronkelijke positie. De gemiddelde waarden over periodes van 3 jaar rond de minima van de TSI tonen t/m de jaren ’80 een correlatie van +0,963 [p=0,000] met de zeewateroppervlaktetemperatuur; de correlatie tussen CO2 en de temperatuur bedraagt voor dezelfde periode slechts +0,656 [p=0,000]. Via een regressie analyse is vastgesteld dat de combinatie van de TSI en CO2 de verklaarde variantie t/m de jaren ’80 niet verhoogd t.o.v. de verklaarde variantie t.g.v. de TSI afzonderlijk; dit blijkt ook het geval wanneer hierbij tevens de invloed van aerosolen in de stratosfeer [AOD6] en de ENSO [ENS ONI7] in beschouwing wordt genomen. Dit impliceert dat de vermeende ‘footprint’ van CO2 getalsmatig geheel ontbreekt in de jaren rond de zonneminima t/m de jaren ’80.
Het verband tussen de TSI aan de top van de atmosfeer en de temperatuur gaat gepaard met een zonnegevoeligheid van 1,2 °C per W/m2 voor het 3-jaren gemiddelde rond de minima van de zonnecyclus; dit verband verklaart de gehele opwarming tussen de 3-jarige periodes rond de primaire zonneminima jaren 1996 en 2017. Dit verband impliceert dat de zon verantwoordelijk is geweest voor ongeveer 1,1 °C van de opwarming die sinds het Maunder minimum aan het einde van de 17de eeuw is ontstaan.
Afgelopen 300 jaar is bij benadering in totaal ruim 1,5 °C opwarming ontstaan bij de oppervlaktetemperatuur van het zeewater; de mondiale temperatuurstijging ligt 0,15-0,30 °C hoger met een waarde van ruim 1,65 °C op basis van de HadCRUT4 en hooguit 1,80 °C op basis van de GISSTEMPv4. Van deze opwarming wordt 1,1 °C toegeschreven aan de zon en 0,3 °C aan de ozonproblematiek. Getalsmatig blijkt voor afgelopen 130 jaar rond de minima de combinatie van de TSI en ozon8 96% van de variantie in de temperatuur te verklaren.
Voor de zeewateroppervlaktetemperatuur resteert een onverklaarde opwarming in de orde van 0,1 °C. Hierbij kan CO2 een rol hebben gespeeld al dan niet in combinatie met andere factoren die relatief weinig invloed hebben gehad op de langetermijntrend zoals: de ENSO, AOD en aerosolen in de lagere atmosfeer. Ook wordt aangetoond dat bij 4 TSI data sets & 4 temperatuur data sets in het pre-satelliet tijdperk rond de primaire minima hetzelfde patroon wordt aangetroffen; in het satelliet tijdperk vormt de PMOD-ACRIM controverse een cruciale kwestie.
In de context van dit onderzoek is van belang dat door het IPCC in AR5 (2013) wordt erkend dat de fase van de zonnecyclus tijdens de minima zowel “meer stabiel” als “meer relevant” is dan bij de maxima het geval is9. Onder klimaatexperts bestaat consensus dat de warmteinhoud van het oceaan systeem een “meer betrouwbare” indicator vormt voor de opwarming dan de opwarming van de atmosfeer10-12; logischerwijs vormt de opwarming van de zeewateroppervlaktetemperatuur daarom zeer waarschijnlijk een meer relevante indicator. Op basis van de wet van Henry is een klein deel (~15%) van de stijging van de CO2 concentratie in de atmosfeer het gevolg van de temperatuurstijging van het oceaan water13-14; tevens is bekend dat in het perspectief van de natuurlijke cycli CO2 de temperatuur volgt en dus niet andersom.
TIP: Figuur 10B beschrijft dat sinds het einde van de 19de eeuw rond de minima van de zonnecyclus de totale zonnestraling voortdurend is gevolgd door de zeewateroppervlaktetemperatuur met uitzondering van de periode tussen midden jaren ’80 en midden jaren ’90.
INHOUD
• I – CO2 toont vergelijkbare karakteristieke dynamiek in relatie tot zowel temperatuur als totale zonnestraling
• II – Zeewateroppervlaktemperatuur en TSI tonen rond zonneminima jaren een vergelijkbaar hoge correlatie met CO2
• III – Na correctie toont zon bijna perfecte correlatie met zeewateroppervlaktetemperatuur voor periode t/m midden jaren ’80
• IV – Zon verklaart t/m jaren ’80 maar liefst 93% variantie zeewateroppervlaktetemperatuur
• V – Sinds eind 19de eeuw verklaren zon en ozon 96% variantie zeewateroppervlaktetemperatuur
• VI – Sinds de 17de eeuw zorgde de zon voor ~1,1 °C opwarming v/d zeewateroppervlaktetemperatuur
• VII – Pre-satelliet tijdperk: rond primaire minima tonen andere data sets hetzelfde profiel
• VIII – Satelliet tijdperk: ACRIM-PMOD controverse cruciaal voor invloed van zon
• IX – Fysische onderbouwing voor invloed zon is conceptueel eenvoudiger dan de CO2-hypothese
• X – Discussie & conclusie
• Referenties
(Data: Excel data file)
I – CO2 toont vergelijkbare karakteristieke dynamiek in relatie tot zowel temperatuur als totale zonnestraling
Figuur 1 betreft een grafiek van KNMI onderzoeker Geert Jan van Oldenborgh waarin het statistische verband tussen de mondiale temperatuur [GISS] en CO2 wordt beschreven. De correlatie tussen beide factoren bedraagt 0,942 [p=0,000; het significantieniveau is bepaald m.b.v. PSPP]. Van Oldenborgh heeft dit verband in zijn grafiek geïllustreerd met een roze trend lijn. Voor de periode 1880-1970 is de correlatie tussen CO2 en de GISS temperatuur overigens aanzienlijk lager, namelijk: 0,616 [p=0,000]. Deze correlaties zeggen echter niets over het mogelijke onderlinge verband tussen temperatuur en CO2 in termen van oorzaak en gevolg. Van Oldenborgh veronderstelt hierbij dat de temperatuurstijging grotendeels het gevolg is van het broeikasgas CO21. Echter, de wet van Henry beschrijft een omgekeerde relatie tussen beide factoren want de concentratie van CO2 in de atmosfeer is o.a. afhankelijk van de temperatuur van het zeewateroppervlak. Dit impliceert dat het oceaan systeem minder goed in staat is om CO2 te absorberen vanuit de atmosfeer wanneer de temperatuur van het zeewater stijgt. Een analyse van de dynamiek tussen beide factoren is logischerwijs dus gewenst om de aard van het statistische verband vast te stellen en te begrijpen.
In dit onderzoek wordt de dynamiek tussen temperatuur en CO2 nader bestudeerd op basis van de meest stabiele fase van de zonnecyclus, namelijk: de zonneminima. In figuur 1 is het verloop van de primaire en secundaire zonneminima jaren met respectievelijk donker en lichtblauw geaccentueerd; uit de waarden blijkt dat t/m 1985 de temperatuur tijdens de secundaire minima voortdurend iets hoger is geweest dan tijdens de direct omringende primaire minima. Aan het einde van deze paragraaf zal blijken dat de zon een tegenovergesteld fenomeen toont; vervolgens zal in paragraaf III een correctie worden geïntroduceerd om de impact van deze tegengestelde fenomenen te neutraliseren.
Figuur 1: CO2 toont een sterke correlatie (r = 0,942 [p=0,000]) met de GISS temperatuur data set; de omvang van de correlatie zegt echter niets over het oorzakelijke verband want de periode 1880-1970 toont bijvoorbeeld een aanzienlijk lagere correlatie (r = 0,616 [p=0,000]). Op basis van de LISIRD TSI data set zijn de primaire en secundaire minimum jaren weergegeven met respectievelijk donker en lichtblauwe kleur.
De GISS data set die van Oldenborgh gebruikt om de relatie tussen CO2 en de temperatuur te bestuderen begint in het jaar 1880; daarom is ook in dit onderzoek de aandacht volledig gericht op de periode vanaf het jaar 1880. De analyse zal hierbij in eerste instantie zijn gericht op een 40-tal jaren bestaande uit 3-jarige periodes rond de minima van de 22-jarige magnetische zonnecyclus volgens de LISIRD TSI data set. Het jaar 1880 betreft geen zonneminimum jaar echter dit jaar volgt direct na het secundaire minimum jaar 1879. Het jaar 1880 vormt daarom onderdeel van de analyse, net als alle jaren direct voor en na de in totaal 13 minimum jaren (dit betreffen 7 primaire minima & 6 secundaire minima) zoals beschreven door de LISIRD TSI data set.
In navolging van figuur 1 beschrijft ook figuur 2 de relatie tussen temperatuur en CO2, doch hierbij is de GISS temperatuur data set vervangen door de HadCRUT415 temperatuur serie. Voor de gehele periode 1880-2018 bedraagt de correlatie tussen de HadCRUT4 en CO2 0,918 [p=0,000], wat slechts iets lager is dan bij de GISS temperatuur data set en CO2 het geval is. Voor de periode 1880-1970 bedraagt de HadCRUT4-CO2 correlatie 0,713 [p=0,000], wat duidelijk een orde van grootte hoger is dan voor dezelfde periode tussen de GISS en CO2 het geval is (r = 0,616 [p=0,000]).
Hieruit blijkt dat de HadCRUT4 een meer stabiele correlatie beschrijft met CO2 dan bij de GISS het geval is; immers, het correlatie verschil tussen beide periodes is bij de HadCRUT4 (verschil 0,918 – 0,713 => levert 0,205) duidelijk kleiner dan bij de GISS (verschil 0,942 – 0,616 => levert 0,326) het geval is. Getalsmatig kan op basis van deze vergelijking worden gesteld dat de instabiliteit van het verband tussen temperatuur en CO2 bij de GISS 59% [= (0,326-0,205)/0,205] hoger is t.o.v. bij de HadCRUT4.
Figuur 2: CO2 toont ook een sterke correlatie met de HadCRUT4 temperatuur data set (r = 0,918 [p=0,000].
Figuur 2 beschrijft dat het verloop van zowel de primaire als secundaire minimum jaren bij benadering representatief is voor het verloop van de gehele data set. Beide minima series tonen een oscillerend patroon waarbij een magnetische zonnecyclus die gepaard gaat met een temperatuurdaling wordt gevolgd door twee opeenvolgende magnetische zonnecycli waarbij de temperatuur stijgt. Naast deze karakteristieke dynamiek tonen de primaire en secundaire minima ook duidelijke verschillen. Bij de secundaire minima is het temperatuurverschil over de dubbele magnetische cyclus in de periode 1902-1943 vrijwel even groot als bij de drievoudige magnetische cyclus in de periode 1943-2008; het gaat hierbij om waarden van respectievelijk: +0,398°C in 41 jaar vs. +0,399°C in 65 jaar. De primaire minima tonen daarentegen tijdens de laatste 2 magnetische cycli in de periode 1976-2017 (41 jaar) een temperatuurstijging aangetroffen die ongeveer 3x groter is dan tijdens de dubbele magnetische cyclus in de periode 1912-1954 (42 jaar). Kortom, de richting van de beweging toont een sterke parallel tussen de primaire en secundaire minima maar de verhoudingen m.b.t. de omvang van de temperatuurverschillen verschilt wel sterk tussen beide series.
Figuur 3 beschrijft het verband voor de HadSST3 zeewateroppervlaktetemperatuur serie en CO2. Voor de gehele periode 1880-2018 bedraagt de correlatie tussen de HadSST3 en CO2: 0,878 [p=0,000], wat iets lager is dan bij de eerder beschreven mondiale temperatuur series (HadCRUT4 en GISS) het geval is. Voor de periode 1880-1970 bedraagt de correlatie: 0,710 [p=0,000], wat vrij nauwkeurig overeenkomt met de HadCRUT4 temperatuur serie. Dit impliceert dat de HadSST3 vs. CO2 combinatie een iets stabielere correlatie toont (verschil 0,878 – 0,710 => levert 0,168) t.o.v. de beide mondiale temperatuur series; de instabiliteit van de correlatie bij de GISS is zelfs 94% hoger dan bij de HadSST3 het geval is.
Ook figuur 3 toont een beeld waarbij beide minima series een oscillatie patroon tonen waarbij na een magnetische zonnecyclus die gepaard gaat met een temperatuurdaling twee opeenvolgende magnetische zonnecycli volgen waarbij de temperatuur stijgt. Naast deze karakteristieke dynamiek tonen de primaire en secundaire minima ook hier duidelijke verschillen, ofschoon deze verschillen in het perspectief van de HadSST3 zeewateroppervlaktetemperatuur iets kleiner zijn t.o.v. de mondiale HadCRUT4 temperatuur serie.
Figuur 3: CO2 toont ook een sterke correlatie met de HadSST3 temperatuur data set (r = 0,878 [p=0,000]).
Uit bovenstaande beschrijving blijkt dat voorafgaand aan het jaar 1970 de omvang van de correlaties tussen CO2 en de diverse temperatuur series duidelijk lager is t.o.v. de correlatie voor gehele periode vanaf 1880. Bovendien blijkt uit figuur 3 dat de temperatuurstijging van het zeewateroppervlak tijdens de 41 jaar tussen de secundaire minima van 1902 en 1943 (+0,408 °C) zelfs duidelijk groter is dan de temperatuurstijging tijdens de 43 jaar tussen 1965 en 2008 (+0,368 °C). Dit vormt een concrete aanwijzing dat CO2 niet grotendeels verantwoordelijk kan zijn geweest voor de temperatuurstijging gedurende beide periodes.
Bij de primaire minima valt in figuur 3 ook op dat de snelheid van de temperatuurstijging in de 20-jarige periode tussen 1976 en 1996 nauwelijks lager is dan in de 21 jarige periode tussen 1996 en 2017. Ook dit vormt een concrete aanwijzing dat CO2 ook hierbij niet grotendeels verantwoordelijk kan zijn geweest voor de temperatuurstijging tijdens beide periodes.
De karakteristieke dynamiek blijkt zelfs niet exclusief gebonden aan de minima jaren van de zonnecyclus, want de twee paarse curves in figuur 4 maken duidelijk dat het karakteristieke patroon zich ook manifesteert bij de waarden op basis van het 3-jarig gemiddelde rond de minima.
De onderste twee blauwe curves in figuur 4 maken duidelijk dat de karakteristieke dynamiek zich ook manifesteert bij de totale zonnestraling. Want de primaire minima series van de TSI tonen immers bij benadering een soortgelijk patroon waarbij na een daling van de primaire TSI minima gedurende een zonnecyclus twee opeenvolgende magnetische zonnecycli volgen waarbij de TSI stijgt. Hierbij valt nog wel op dat de TSI secundaire minima een afwijking toont in het patroon bij de overgang van de periode 1901-1903 naar de periode 1921-1923 omdat hierbij een (kleine) daling wordt aangetroffen, terwijl de temperatuur bij de secundaire minima van deze overgang daarentegen een stijging toont.
Figuur 4: De totale zonnestraling (TSI) toont op basis van het 3-jarige gemiddelde rond de minima vrijwel hetzelfde karakteristieke patroon dat zich ook bij de temperatuur manifesteert. Enkel de secundaire minima tonen bij de eerste overgang van de temperatuur en de TSI een verschil in de richting van de trend.
Een opvallend verschil tussen de zeeoppervlaktewatertemperatuur en de TSI is dat in het laatste perspectief de curve met de secundaire TSI waarden grotendeels duidelijk onder de primaire TSI waarden ligt. In de periode t/m de jaren ’80 ligt de curve van de secundaire temperatuur waarden daarentegen grotendeels boven de primaire temperatuur waarden. Dit wijst in de richting van de mogelijkheid dat de samenstelling van de zonnestraling tijdens de primaire en secundaire zonneminima mogelijk wezenlijk van elkaar verschilt waardoor een lagere TSI gepaard kan gaan met hoge temperaturen. Dit fenomeen toont een duidelijke parallel met de Gnevyshev-Ohl regel16, waarvan bekend is dat deze gepaard gaat met zonne-proton gebeurtenissen en structurele veranderingen in het magnetische veld van de zon17 – dit veld is bepalend voor de hoeveelheid kosmische straling die de aarde kan bereiken. Logischerwijs speelt de magnetische cyclus van de zon dus ook een rol bij de samenstelling van de atmosfeer van de aarde en beïnvloed via dit mechanisme ook het klimaat18.
Figuur 4 toont voor beide perspectieven een trendkanaal in de vorm van gele zones dat is gebaseerd op de primaire minima, ofwel: de meeste stabiele fase van de zonnecyclus. Immers, enkel bij de primaire minima bevinden de polen van de zon zich in de oorspronkelijke positie; de polen zijn daarentegen van positie gewisseld bij de secundaire minima. Enkel bij de TSI liggen de gemiddelde waarden van de laatste twee primaire periodes (1984-86 en 2016-18) binnen het bijbehorende trendkanaal, terwijl bij de zeeoppervlaktewatertemperatuur de gemiddelde waarde van de laatste twee primaire periodes zich ruim boven het trendkanaal bevinden. Een bevestiging hiervoor vormt de relatief grote afstand tussen de temperatuur en de TSI bij deze periodes. Het grootste verschil tussen de temperatuur en de TSI manifesteert zich bij de overgang tussen de primaire jaren 1975-77 en 1995-97: enkel de temperatuur is gedurende deze overgang duidelijk opgelopen terwijl de TSI slechts een minimale stijging toont.
Ook blijkt uit figuur 4 tevens dat de afstand tussen de temperatuur en de TSI in de periode t/m de periode 1984-86 stabiel is gebleven. Dit suggereert dat opwarming bovenop de impact van de geleidelijk toegenomen activiteit van de zon ogenschijnlijk pas na de midden jaren ’80 duidelijk is ontstaan. Hierbij kunnen we hierbij vaststellen dat zowel bij de temperatuur als de TSI de waarde voor de secundaire periode 1984-86 nog duidelijk lager ligt t.o.v. de secundaire periode 1942-44 (nadat in beide perspectieven de waarde voor de periode 1964-66 slechts iets lager ligt dan de periode 1984-86).
De aantasting van de ozonlaag + het ontstaan van het seizoensgerelateerde gat in de ozonlaag bij de zuidpool heeft zich vanaf het jaar 1979 aangediend. Omdat de ozonlaag verantwoordelijk is voor het blokkeren van ultraviolete [UV] zonnestraling – waardoor een groot deel van het hoogfrequente deel van de zonnestraling het aardoppervlak niet kan bereiken – betekent dit dat de aantasting van de ozonlaag een bijdrage heeft geleverd aan de opwarming van de lagere atmosfeer. Figuur SPM.5 in IPCC AR5 bevestigt dat ozon [O3] een significante bijdrage levert aan de opwarming van de atmosfeer want O3 speelt m.b.t. de stralingsforcering een rol bij maar liefst 5 antropogene emitters, met in 4 gevallen een bijdrage aan de toename van de stralingsforcering19; de grootste bijdrage wordt aangetroffen in relatie tot methaan [CH4].
In navolging van figuur 4 beschrijft paragraaf II dat rond de zonneminima jaren de correlatie tussen CO2 en de zeewateroppervlaktetemperatuur ongeveer even hoog is als de correlatie tussen CO2 en de TSI. Vervolgens wordt in paragraaf III en IV op basis van een twee verschillende analyse technieken beschreven dat de combinatie van zon en ozon de geleidelijke opwarming van de afgelopen 130 jaar grotendeels verklaard.
II – Zeewateroppervlaktetemperatuur en TSI tonen rond zonneminima jaren een vergelijkbaar hoge correlatie met CO2
Nadat in de eerste paragraaf de aandacht werd gericht op een beschrijving van de dynamiek die zichtbaar is bij de minima jaren wordt in het vervolg de blik verruimt door ook de jaren direct voor en na de minima in de analyse te betrekken. Figuur 5 beschrijft dat de correlatie tussen de zeewateroppervlaktetemperatuur en CO2 in de periode vanaf 1880 bij de primaire minima jaren + de direct omringende jaren vrijwel dezelfde omvang toont als de correlatie tussen de zeewateroppervlaktetemperatuur en TSI. Deze correlaties hebben betrekking op in totaal 21 jaren rond de primaire minima; de omvang bedraagt respectievelijk voor zeewateroppervlaktetemperatuur & CO2: 0,916 [p=0,000] en voor zeewateroppervlaktemperatuur & TSI: 0,902 [p=0,000].
Voor de periode t/m eind jaren ’70 blijkt in figuur 5 enkel de correlatie tussen TSI & CO2 met een waarde van 0,813 [p=0,000] niet veel lager te zijn dan voor de gehele periode. Daarentegen is de correlatie tussen temperatuur & CO2 met een waarde van 0,544 [p=0,018] wel duidelijk fors lager t.o.v. de gehele periode.
Figuur 5: Bij de 21 jaren rond de primaire zonneminima voor de gehele periode vanaf het jaar 1880 toont de zeewateroppervlaktetemperatuur [HadSST3] met CO2 een correlatie (0,916 [p=0,000]) van vergelijkbare omvang t.o.v. de correlatie (0,902 [p=0,000]) voor de combinatie van zeewateroppervlaktetemperatuur en TSI [LISIRD]. De periode t/m de jaren ’70 maakt duidelijk dat de zeewateroppervlaktetemperatuur enkel in relatie tot de TSI een stabiele correlatie toont t.o.v. de gehele periode; bij CO2 ligt de correlatie voor deze periode bij de primaire minima op een veel lager niveau.
Vervolgens toont figuur 6 voor de secundaire jaren + de direct omringende jaren dat de correlatie tussen zeewateroppervlaktetemperatuur en CO2 in de periode vanaf 1880 exact dezelfde omvang heeft als de correlatie tussen zeewateroppervlaktetemperatuur en TSI. Deze correlaties hebben betrekking op in totaal 19 jaren en hebben beide een omvang van 0,832 [p=0,000].
Voor de periode t/m de jaren ’70 blijkt ook rond de secundaire minima de correlatie bij de TSI met een waarde van 0,808 [p=0,000] niet veel lager te zijn t.o.v. de gehele periode. Terwijl de correlatie bij CO2 met een waarde van 0,633 [p=0,010] opnieuw fors lager is t.o.v. de gehele periode. Kortom, de primaire en secundaire jaren tonen afzonderlijk ongeveer hetzelfde totaalbeeld: enkel voor de combinatie van de zeewateroppervlaktetemperatuur en TSI wordt een stabiele correlatie aangetroffen.
Figuur 6: Bij de 19 jaren rond de secundaire zonneminima voor de gehele periode vanaf het jaar 1880 toont de zeewateroppervlaktetemperatuur [HadSST3] met CO2 een correlatie (0,832 [p=0,000]) met exact dezelfde omvang als de correlatie bij de combinatie van zeewateroppervlaktetemperatuur en TSI. De periode t/m de jaren ’70 maakt duidelijk dat de zeewateroppervlaktetemperatuur enkel in relatie tot de TSI een stabiele correlatie toont t.o.v. de gehele periode; voor CO2 ligt de correlatie voor deze periode bij de secundaire minima op een beduidend lager niveau.
Wanneer vervolgens de primaire en secundaire jaren worden samengevoegd dan blijkt uit figuur 7 dat het totaalbeeld nauwelijks veranderd t.o.v. de primaire en secundaire jaren afzonderlijk. Voor de 40 jaren verspreid over de gehele periode toont de correlatie tussen de zeewateroppervlaktetemperatuur en CO2 een waarde van 0,885 [p=0,000], welke slechts in beperkte mate afwijkt van de gemiddelde correlatie bij de primaire en secundaire jaren afzonderlijk. De omvang van de correlatie tussen de zeewateroppervlaktetemperatuur en de TSI heeft bij benadering een waarde van vergelijkbare omvang, ofschoon deze correlatie met een waarde van 0,841 [p=0,000] wel iets lager ligt.
M.b.t. de periode t/m eind jaren ’70 ligt de correlatie waarde bij CO2 (r = 0,547 [p=0,001]) voor de combinatie van de primaire en secundaire minima opnieuw een stuk lager dan bij de TSI (r = 0,728 [p=0,000]) het geval is.
Figuur 7: Bij de 40 jaren rond de zonneminima voor de periode vanaf het jaar 1880 toont de zeewateroppervlaktetemperatuur [HadSST3] een correlatie in dezelfde orde van grootte t.o.v. zowel CO2 (r = 0,885 [p=0,000]) als de TSI (r = 0,841 [p=0,000]).
Uit figuur 5 t/m 7 blijkt dat voor de jaren rond de minima van de zonnecyclus de hoge correlatie tussen de zeewateroppervlaktetemperatuur en CO2 geenszins uniek is. Want zowel bij de primaire minima, de secundaire minima en ook bij de combinatie van beide minima series toont de correlatie tussen zeewateroppervlaktetemperatuur en TSI voortdurend een omvang van vergelijkbare grootte. Bovendien blijkt uit de waarden in de 100-jarige periode tussen 1880 en eind jaren ’70 dat de correlatie van de temperatuur met de zon duidelijk meer stabiel is dan de correlatie met CO2.
In dit perspectief is tevens van belang dat enkel m.b.t. de correlatie tussen de TSI en de zeewateroppervlaktetemperatuur geen onduidelijkheid bestaat in termen van oorzaak en gevolg. Hierbij kunnen we hooguit speculeren over de mogelijkheid dat de beschreven verbanden berusten op een spurieus verband – ofschoon er fundamenteel bezien geen concrete aanleiding is om te veronderstellen dat hiervan daadwerkelijk sprake is want de zon vormt immers de drijvende kracht achter het klimaat.
Bij de correlatie tussen CO2 en de zeewateroppervlakte temperatuur is daarentegen geenszins sprake van een eenduidig mechanisme in termen van oorzaak en gevolg. Want enerzijds heeft CO2 als broeikasgas de potentie om zelf een bijdrage te leveren aan een temperatuurstijging. Doch, anderzijds blijkt uit de wet van Henry dat een toename van de temperatuur van het oceaan systeem kan leiden tot een hogere waarde van CO2 in de atmosfeer. Er is hierbij in potentie dus sprake van een inconsistentie. Overigens, de broeikastheorie wordt anno 2020 vooral gedragen op basis van ‘consensus’ terwijl deze theorie op basis van empirische data eigenlijk geenszins als ‘bewezen’ kan worden beschouwd. In 2015 werd zelfs pas het eerste empirisch bewijs geclaimd waaruit blijkt dat CO2 enige invloed (~10% van de trend) heeft bij de ’terugstraling’ van lange golf straling (infraroodstraling) vanuit de atmosfeer20. Een kanttekening vormt hierbij dat van de natuurlijke cycli bekend is dat CO2 de temperatuur volgt en niet andersom. Dit is van toepassing op zowel korte als de lange termijn cycli, zoals: de dagelijkse cyclus21, de seizoenscyclus21 en de ijstijden cyclus22.
Tenslotte toont figuur 7 nog een belangrijk detail. Want enkel bij de TSI toont de periode t/m de jaren ’70 een duidelijk lagere correlatie nadat de beide minima series zijn samengevoegd (r = 0,728 [p=0,000]); terwijl uit figuur 5 & 6 blijkt dat de correlaties bij de primaire minima (r = 0,813 [p=0,000]) en de secundaire minima (r = 0,808 [p=0,000]) afzonderlijk duidelijk op een hoger niveau liggen. In de volgende paragraaf zal blijken dat dit fenomeen via een correctie (gericht op de secundaire minima) eenvoudig kan worden geneutraliseerd; na toepassing van de correctie zal blijken dat voor de temperatuur en de zon bij de gemiddelde waarden over 3 jaar rond de minima zelfs een bijna perfecte correlatie ontstaat voor de periode t/m de jaren ’80.
III – Na correctie toont zon bijna perfecte correlatie met zeewateroppervlaktetemperatuur voor periode t/m midden jaren ’80
In de eerste paragraaf beschrijft figuur 4 dat binnen de 22-jarige magnetische zonnecyclus tussen de primaire en secundaire minima een structureel fenomeen wordt aangetroffen dat een parallel oplevert met de regel van Gnevyshev-Ohl (dit betreft een regel die overigens zelf enkel betrekking heeft op het aantal zonnevlekken bij de maxima). De secundaire TSI waarden blijken zich op een structureel lager niveau te bevinden dan de primaire TSI waarden; echter, bij de temperatuur is een tendens zichtbaar in de tegenovergestelde richting. Vervolgens heeft figuur 7 in de tweede paragraaf duidelijk gemaakt dat bij het samenvoegen van de primaire en secundaire minima een deel van de correlatie tussen de zeewateroppervlaktetemperatuur en de TSI verloren gaat – dit effect is vooral bij de periode t/m de jaren ’70 duidelijk zichtbaar.
Via een eenvoudige correctie gericht op de secundaire minima (waarbij de TSI waarden met +0,123 W/m2 zijn verhoogd) kan de daling van de correlatie ongedaan worden gemaakt. Figuur 8 beschrijft het resultaat na de correctie (de correctie heeft enkel betrekking op het rechtse panel van figuur 7; het linker panel van figuur 7 is in figuur 8 ongewijzigd gebleven). Na toepassing van de correctie blijkt de correlatie tussen zeewateroppervlaktetemperatuur en TSI voor de combinatie van de beide minima series in de periode t/m de jaren ’70 te stijgen naar een waarde van 0,813 [p=0,000]. Na de correctie komt deze correlatie exact overeen met de correlatie waarde van de primaire minima (0,813 [p=0,000]); de afwijking van de correlatie waarde bij de secundaire minima (0,808 [p=0,000]) blijkt hierbij ook zeer gering. Bovendien blijkt na toepassing van de correctie dat voor de gehele periode de correlatie voor de combinatie van de primaire en secundaire minima (0,874 [p=0,000]) ook iets is gestegen t.o.v. de waarde zonder de correctie (figuur 7 toont voor de combinatie van de primaire en secundaire minima voor de gehele periode een correlatie met een waarde van 0,841 [p=0,000]).
Figuur 8: Na verhoging van de secundaire minima met 0,123 W/m2 blijkt voor de periode t/m de jaren ’70 de correlatie tussen zeewateroppervlaktetemperatuur en TSI bij de combinatie van de beide minima series hersteld tot een waarde van 0,813 [p=0,000]; deze gecorrigeerde correlatie waarde komt exact overeen met de waarde bij de primaire minima (0,813 [p=0,000]) en de afwijking is bovendien zeer gering t.o.v. de waarde bij de secundaire minima (0,808 [p=0,000]).
Figuur 8 beschrijft tevens dat de temperatuur impact van de zon tijdens de meest recente periode vanaf de jaren ’90 rond de minima een gemiddelde waarde toont van 1,14 °C per W/m2; deze waarde komt bij benadering overeen met de gemiddelde waarde van 1,08 °C per W/m2 die wordt aangetroffen voor de jaren rond de minima in de periode 1880-1980’s. Diverse tussenliggende periodes tonen bovendien waarden met dezelfde orde van grootte.
Ook tonen de correlaties tussen temperatuur en zon bij een vergelijking tussen de periode t/m de 1970’s en de gehele periode een zeer hoog niveau van consistentie (verschil 0,874 – 0,813 => levert 0,061); terwijl de correlatie tussen temperatuur en CO2 bij een vergelijking tussen beide periodes een laag niveau van consistentie toont (verschil 0,885 – 0,547 => levert 0,338).
In navolging van figuur 8 wordt in figuur 9 het beeld getoond dat na de correctie ontstaat op basis van de 3-jarig gemiddelde waarden rond de minima. Het linker panel van figuur 9 toont voor CO2 dezelfde karakteristieke dynamiek met een oscillerende beweging die in paragraaf I voor de individuele primaire minima en secundaire minima jaren afzonderlijk is beschreven; deze dynamiek blijft dus behouden in het perspectief van het 3-jarig gemiddelde rond de minima.
In het rechter panel van figuur 9 toont de zon een bijna perfecte correlatie met de temperatuur over de gehele periode met uitzondering van de overgang tussen de minima periodes in de jaren ’80 en ’90. Van belang is dat de periode vanaf 1979 t/m de midden jaren ’90 bekend staat als het tijdspanne waarin de ozon problematiek is ontstaan. In 1991 bereikte de ozonconcentratie voor het eerst het niveau van 100 DU en enkele jaren later volgde in 1994 het dieptepunt; vanaf de eind jaren ’90 zijn de ozon niveaus vervolgens gestabiliseerd23.
Figuur 9: Na toepassing van de correctie (gericht op de secundaire minima: +0,123 W/m2) toont het 3-jarig TSI gemiddelde rond de minima voor de zon een bijna perfecte correlatie met de zeewateroppervlaktetemperatuur gedurende bijna de gehele periode; enkel de overgang tussen de minima jaren in de jaren ’80 en ’90 toont een inconsistent verloop tussen beide factoren. Deze inconsistentie valt samen met het tijdspanne waarin het aan de seizoenen gerelateerde gat in de ozonlaag bij de zuidpool is ontstaan.
Figuur 9 toont een opmerkelijk beeld want zowel voor de periodes t/m midden jaren ’70, de periode t/m de jaren ’80, als ook de gehele periode toont de combinatie van de zeewateroppervlaktetemperatuur en de totale zonnestraling een bijna perfecte correlatie. Bovendien blijkt dat de correlaties op basis van het 3-jarig gemiddelde rond de minima tussen temperatuur en CO2 (zie linker panel) voor alle drie de periodes consequent lager zijn dan de correlaties tussen temperatuur en totale zonnestraling (zie rechter panel). Enkel de correlaties met de zon tonen voor alle drie de periodes een stabiel beeld; hieruit blijkt dat de zon een onderliggende verklarende factor vormt voor het ontstaan van de sterke statistische correlatie tussen CO2 en de temperatuur. Kortom, de stabiele consistente correlaties tussen de zon en de temperatuur tonen aan dat de zon logischerwijs grotendeels verantwoordelijk is geweest voor de temperatuurstijging (in paragraaf VI wordt de mogelijkheid dat CO2 hierbij ook een rol heeft gespeeld nader onderzocht).
In figuur 10 wordt de impact van de correctie op basis van de 22-jarige zonnecyclus (via de secundaire TSI minima) op een meer directe manier visueel weergegeven voor de waarden op basis van het 3-jarig gemiddelde. Figuur 10A en 10B beschrijven respectievelijk het beeld zonder en met de correctie; figuur 10C beschrijft vervolgens de impact nadat de (inconsistente) overgang tussen de minima periodes in de jaren ’80 en ’90 is geneutraliseerd.
Uit figuur 10 blijkt dat de 3-jarige periodes rond de minima via slechts 2 stappen (lees: 2 correcties) een consistente en tevens ‘bijna perfecte correlatie’ tonen m.b.t. de combinatie van de zon en de temperatuur voor de gehele periode. De verhouding tussen de schalen voor de temperatuur en de totale zonnestraling is vastgesteld m.b.v. een regressie analyse op basis van de 3-jarige waarden voor de minima in de periode t/m de jaren ’80 (dit betreft data over een tijdspanne van bijna 100 jaar vanaf de 3-jarige periode rond het primaire minimum in 1890). Deze verhouding komt overeen met een zonnegevoeligheid van 1,26 °C per W/m2 op basis van de TSI aan de top van de atmosfeer (in paragraaf IX wordt een getalsmatige beschrijving gegeven voor het perspectief van het aardoppervlak + de noodzaak van een natuurkundig versterkend mechanisme voor de invloed van de zon).
Figuur 10: Na correcties voor de 22-jarige magnetische zonnecyclus en de ozonproblematiek toont de totale zonnestraling een consistente en ‘bijna perfecte correlatie’ met de zeewateroppervlaktetemperatuur. Figuur 10A toont de 3-jarig gemiddelde minima waarden voor de LISIRD TSI en HadSST3 zeewateroppervlaktetemperatuur; in figuur 10B zijn de secundaire [S] TSI waarden verhoogd met een waarde van +0,123 W/m2 (= een correctie i.v.m. de omwisseling van de magnetische polen in het perspectief van de 22-jarige zonnecyclus); tenslotte is in figuur 10C een 2de correctie toegepast (i.v.m. ozonproblematiek) waarbij de impact van de overgang tussen de periode 1984-86 en 1995-97 is geneutraliseerd bij de laatste 3 minima periodes.
Figuur 10 beschrijft dat afgezien van het deel van de opwarming dat is ontstaan t.g.v. de ozonproblematiek (impact: 0,266 °C), het restant (impact: 0,548 °C) van de totale opwarming (impact: 0,814 °C) bij benadering in potentie geheel kan worden verklaard door de zon – na toepassing van de correctie gericht op de secundaire minima [S]. Want zowel figuur 10A als figuur 10B beschrijft dat de zon afgelopen 130 jaar in het perspectief van de primaire minima [P] heeft gezorgd voor een opwarming van 0,581 °C en de combinatie van figuur 10B & 10C beschrijft indicatief dat de zon in combinatie met de ozonproblematiek voor 0,847 °C (= 0,581 °C + 0,266 °C) opwarming heeft gezorgd. Opvallend bij figuur 10C is dat de afwijking tussen de temperatuur en de TSI enkel bij de eerste 5 minima periodes (1890s t/m 1930s) relatief groot is t.o.v. de relatief kleine verschillen bij de laatste 7 minima periodes (1940s t/m 2010s).
Echter, in figuur 10 is nog geen rekening gehouden met de mogelijkheid dat de zon in combinatie met andere factoren mogelijk een groter deel van de variantie zou kunnen verklaren. In de volgende paragrafen zijn erop gericht om dit nader te onderzoeken op basis van 5 klimatologische componenten: TSI, ozon, CO2, AOD & ENSO.
IV – Zon verklaart t/m jaren ’80 maar liefst 93% variantie zeewateroppervlaktetemperatuur
Een analyse gericht op een vijftal klimatologische componenten maakt duidelijk dat de aangepaste TSI (na een correctie gericht op de secundaire minima) weinig ruimte laat voor de invloed van andere factoren. Uit onderstaand overzicht blijkt dat voor de periode t/m de jaren ’80 in het perspectief van het 3-jarig gemiddelde rond de minima maar liefst 93% van de variantie in de zeewateroppervlaktetemperatuur door de aangepast TSI wordt verklaard.
• TSI [LISIRD] met aanpassing (+0,123 W/m2) van de secundaire waarden:
– Volledige periode: R = 0,93; R-kwadraat = 0,87 (verklaarde variantie = 87%); p=0,000
– Periode t/m ’80s: R = 0,96; R-kwadraat = 0,93 (verklaarde variantie = 93%); p=0,000
• TSI [LISIRD] zonder aanpassing van de secundaire waarden:
– Volledige periode: R = 0,89; R-kwadraat = 0,80 (verklaarde variantie = 80%); p=0,000
– Periode t/m ’80s: R = 0,85; R-kwadraat = 0,72 (verklaarde variantie = 72%); p=0,002
• CO2:
– Volledige periode: R = 0,92; R-kwadraat = 0,84 (verklaarde variantie = 84%); p=0,000
– Periode t/m ’80s: R = 0,66; R-kwadraat = 0,44 (verklaarde variantie = 44%); p=0,037
• Ozon (omvang gat in ozonlaag):
– Volledige periode: R = 0,82; R-kwadraat = 0,67 (verklaarde variantie = 67%); p=0,001
– Periode t/m ’80s: (geen analyse mogelijk omdat alle waarden nul bedragen voor deze periode)
• AOD [NASA]:
– Volledige periode: R = 0,30; R-kwadraat = 0,09 (verklaarde variantie = 9%); p=0,323
– Periode t/m ’80s: R = 0,01; R-kwadraat = 0,00 (verklaarde variantie = 0%); p=0,986
• ENSO [ENS ONI met 6 maanden vertraagde impact]:
– Volledige periode: R = 0,11; R-kwadraat = 0,01 (verklaarde variantie = 1%); p=0,712
– Periode t/m ’80s: R = 0,39; R-kwadraat = 0,15 (verklaarde variantie = 15%); p=0,271
Uit dit overzicht blijkt dat op basis van de individuele componenten enkel de TSI meer dan 50% van de variantie van de zeewateroppervlaktetemperatuur t/m de jaren ’80 verklaard; dit geldt voor de TSI zowel met als zonder de correctie.
Tevens is m.b.v. een enkelvoudige regressie analyse [uitgevoerd met het statistiekprogramma PSPP] onderzocht of CO2 in combinatie met de gecorrigeerde TSI een bijdrage kan leveren aan de verklaarde variantie voor de periode t/m de minima periode 1984-86. Dit blijkt niet het geval te zijn want de verklaarde variantie op basis van enkel de gecorrigeerde TSI bedraagt 93%, terwijl de gecorrigeerde TSI in combinatie met CO2 resulteert in een verklaarde variantie van slechts 91% (op basis van ‘bijgestelde R-kwadraat’ waarden); bovendien is de bijdrage van CO2 hierbij niet significant.
Ook is onderzocht in hoeverre de AOD en/of de ENSO al dan niet in combinatie met CO2 een bijdrage levert aan de verklaarde variantie; dit blijkt voor zowel de individuele factoren als alle mogelijke combinaties tussen deze factoren ook niet het geval te zijn. Dit impliceert dat de overige factoren voor de periode t/m de jaren ’80 geen meerwaarde genereren ten opzicht van de impact van de gecorrigeerde TSI.
Overigens, de combinatie van de TSI en CO2 levert ook geen meerwaarde op voor de 72% verklaarde variantie die wordt gevonden op basis van de ongecorrigeerde TSI. Want een regressie analyse wijst uit dat de verklaarde variantie op basis van de bijgestelde R-kwadraat ook daalt naar 70% voor de combinatie van de ongecorrigeerde TSI en CO2. Bovendien levert opnieuw enkel de TSI component een significante bijdrage aan de combinatie. En ook hier blijken combinaties met de AOD en/of de ENSO voor de periode t/m de jaren ’80 in het perspectief van de 3-jarig gemiddelde waarden rond de minima zonder correctie geen meerwaarde te genereren in termen van de verklaarde variantie (op basis van ‘bijgestelde R-kwadraat’ waarden).
V – Sinds eind 19de eeuw verklaren zon en ozon 96% variantie zeewateroppervlaktetemperatuur
In paragraaf III werd een eerste indicatieve inschatting gepresenteerd voor de impact van de aangepaste TSI in combinatie met ozon; hierbij werd impliciet verondersteld dat de impact van de ozonproblematiek sinds de jaren ’90 stabiel is gebleven. Eerder werd in het februari artikel gebruik gemaakt van de omvang van het aan de seizoenen gerelateerde gat in de ozonlaag bij Antarctica8 om de invloed van de verzwakte ozonlaag meer nauwkeurig te bestuderen.
Een regressie analyse gericht op de waarden op basis van het 3-jarig gemiddelde wijst uit dat de aangepaste TSI in combinatie met de omvang van het gat in de ozonlaag een bijgestelde R-kwadraat waarde oplevert van 0,96; dit impliceert dat 96% van de zeewateroppervlaktetemperatuur variantie wordt verklaard door de combinatie van zon en ozon voor de gehele periode rond het minimum jaar 1890. Bovendien leveren beide componenten een hoog significante bijdrage aan dit resultaat (met p-waarde: 0,000). Zonder de correctie gericht op de minima verklaard de combinatie voor de gehele periode 91% van de variantie in de zeewateroppervlaktetemperatuur.
Tevens is onderzocht in hoeverre de componenten CO2, AOD en ENSO voor de gehele periode meerwaarde genereren in termen van de verklaarde variantie binnen het perspectief van de 3-jarig gemiddelde waarden bij de minima. Hiervan blijkt geenszins sprake te zijn; dit geldt overigens voor zowel de TSI waarden zonder correctie als ook de TSI waarden met correctie gericht op de secundaire minima.
VI – Sinds de 17de eeuw zorgde de zon voor 1,1 °C opwarming v/d zeewateroppervlaktetemperatuur
In paragraaf III is m.b.t. figuur 10 (na toepassing van de correctie gericht op de secundaire minima) via een regressie analyse een zonnegevoeligheid beschreven van 1,26 °C per W/m2. Bovendien blijkt uit figuur 10C dat na een aanvullende correctie gericht op de overgang tussen de periode 1984-86 en de periode 1995-97 de zon een indicatieve “bijna perfecte correlatie” toont met de zeewateroppervlaktetemperatuur.
Vervolgens is in paragraaf IV vastgesteld dat na de correctie gericht op de secundaire minima de TSI 93% verklaard van de variantie in de zeewateroppervlaktetemperatuur voor de periode t/m de jaren ’80. En paragraaf V heeft duidelijk gemaakt dat de gecorrigeerde TSI in combinatie met de omvang van het gat in de ozonlaag bij de zuidpool maar liefst 96% verklaard van de variantie over de gehele periode sinds het laatste decennium van de 19de eeuw.
Van belang is dat deze resultaten zijn gebaseerd op waarden over een 3-jarige periode. Wanneer de zonnegevoeligheid voor de gemiddelde waarden over 3 jaar m.b.t. de gehele periode wordt berekend in combinatie met de omvang van het gat in de ozonlaag, dan wordt een waarde aangetroffen van 1,23 °C per W/m2 (verklaarde variantie: 96%).
Echter, wanneer de zonnegevoeligheid wordt berekend op basis van de individuele jaren t/m de jaren ’80 dan wordt voor de zonnegevoeligheid een waarde aangetroffen van 1,07 °C per W/m2 (verklaarde variantie: 63%). En een berekening van de zonnegevoeligheid op basis van de individuele jaren in combinatie met de omvang van het gat in de ozonlaag resulteert in een waarde van 0,96 °C per W/m2 (verklaarde variantie: 84%). Hierbij ontstaat de indruk dat in het perspectief van individuele jaren ‘klimaatruis’ (via bijvoorbeeld fase verschillen) een rol speelt bij het maskeren van de zonnegevoeligheid.
De aangetroffen waarde voor de zonnegevoeligheid is dus wel sterk afhankelijk van de gekozen rekenmethode. Omdat de verklaarde variantie (96%) het hoogste is bij de waarde voor de zonnegevoeligheid van 1,23 °C per W/m2 op basis van het 3-jarig gemiddelde over de gehele periode via de combinatie van de zon en ozon, lijkt de keuze gerechtvaardigd om op basis van deze waarde een inschatting te maken voor de opwarming die de zon sinds het Maunder minimum aan het einde van de 17de eeuw heeft veroorzaakt.
In de tussentijd is de TSI gestegen van een waarde van 1360,274 W/m2 tijdens de minima van de laatste 4 decennia van de 17de eeuw naar een waarde van 1361,215 W/m2 tijdens het meest recente primaire minimum jaar 2017. Dit komt overeen met een stijging van 0,941 W/m2 over een periode van ongeveer 330 jaar.
De stijging van 0,941 W/m2 levert in combinatie met een zonnegevoeligheid van 1,23 °C per W/m2 een temperatuurstijging op van 1,157 °C in 330 jaar. Omgerekend komt dit overeen met een gemiddelde temperatuurstijging van ruim 0,35 °C per eeuw; voor de meest recente periode is de gemiddelde waarde echter 2x groter, want: sinds het 3-jarig minimum rond het jaar 1912 verklaart de zon op basis van de LISIRD ruim 0,7 °C van de opwarming tijdens de afgelopen 110 jaar (waarvan 0,38 °C tussen het 3-jarige minimum rond 1912 en 1996 over een periode van 84 jaar = gemiddeld 0,45 °C per 100 jaar).
* In het februari artikel is vermeld dat Zharkova et al. (24 juni 2019)24 op basis van diverse magnetische eigenschappen van de zon een natuurlijk impact trend van gemiddeld 0,5 °C voor de 20ste eeuw heeft beschreven. Op 4 maart 2020 werd het betreffende artikel door het tijdschrift Nature ingetrokken tegen de zin in van 3 van de 4 auteurs (dit is gebeurd onder druk van bezwaren die voornamelijk betrekking hebben op een gemaakte veronderstelling m.b.t. het bestaan van niet-gecorreleerde fluctuaties in de beweging van de zon en de aarde rond het barycentrum; zowel de omvang als de richting van deze fluctuaties wordt betwist door peer reviewers op basis van de veronderstelling dat de beweging van zon en aarde beide onder dezelfde invloed staat van de planeet Jupiter + enkele andere planeten).
VII – Pre-satelliet tijdperk: rond primaire minima tonen andere data sets hetzelfde profiel
In voorgaande paragrafen is gebleken dat rond de minima het profiel van de LISIRD TSI data set een bijzonder sterke parallel toont met de HadSST3 data set voor de zeewateroppervlaktetemperatuur. In deze paragraaf wordt de combinatie van beide data sets in een breder perspectief geplaatst via een vergelijking met de waarden op basis het 3-jarig gemiddelde rond de primaire minima in het pre-satelliet tijdperk. Hierbij is gebruik gemaakt van in totaal 4 TSI data sets (LISIRD, IPCC AR5, Satire S&T en NRLTSI2) en 4 temperatuur data sets (HadSST3, HadCRUT4, GISSTEMP v4 en GISS SST). Zowel de HadSST3 data set als de GISS SST data set hebben betrekking op de zeewateroppervlaktetemperatuur.
Uit figuur 11 blijkt dat alle 8 data sets voor de primaire minima jaren in het pre-satelliet tijdperk bij benadering hetzelfde profiel tonen. Bij iedere data sets beschrijft het jaar 1912 de laagste waarde; 1890 en 1933 tonen hogere waarden en bij 1954 en 1976 zijn de waarden nog hoger. Opvallend is ook dat de gemiddelde waarden van de 4 TSI data sets enerzijds en de gemiddelde waarden van de 4 temperatuur data sets anderzijds een correlatie tonen van 0,928 [p=0,011].
Figuur 11: Een vergelijking tussen 4 TSI data sets (LISIRD, IPCC AR5, Satire S&T en NRLTSI2) en 4 temperatuur data sets (HadSST3, HadCRUT4, GISSTEMP v4 en GISS SST) toont voor het pre-satelliet tijdperk bij alle data sets hetzelfde patroon rond de primaire minima. Alle data sets tonen de laagste waarde bij de periode rond 1912; 1890 en 1933 tonen hogere waarden en bij 1954 en 1976 worden nog hogere waarden aangetroffen.
Figuur 11 beschrijft ook dat de interne consistentie tussen de 4 TSI data sets iets hoger is dan bij de 4 temperatuur data sets het geval is. Dit kan in potentie deels worden verklaard doordat 2 van de temperatuur data sets betrekking hebben op de temperatuur van het zeewateroppervlak (HadSST3 en GISS SST) en de 2 andere temperatuur data sets betrekking hebben op de mondiale temperatuur (HadCRUT4 en GISSTEMP v4). Echter, het is ook opmerkelijk dat vooral de GISS SST temperatuur data set van de NASA een relatief grote afwijking beschrijft t.o.v. de overige data sets. Dit impliceert dat de GISS SST minder consistent is t.o.v. de overige 6 data sets dan bij de HadSST3 data set het geval is.
Het is ook interessant om vast te stellen dat de correlatie tussen de GISS SST en GISSTEMP v4 met een waarde van 0,942 duidelijk ook minder consistent is dan de correlatie tussen de HadSST3 en de HadCRUT4 welke 0,993 bedraagt. Kortom, de data sets van het Hadley Centre zijn duidelijk meer consistent t.o.v. elkaar dan bij de data sets van de NASA het geval is.
Curieus is dat de GISSTEMP v4 data set met 3 van de 4 TSI data sets in figuur 11 een correlatie toont waarbij de waarde nauwelijks lager is dan de waarde van de correlatie met de bijbehorende GISS SST data set. Bij een onderlinge vergelijking tussen alle 8 data sets kan hieruit worden geconcludeerd dat de GISS SST data set met afstand de grootste afwijking toont. Opvallend is dat de afwijking tussen de GISS SST en de twee temperatuur data sets van het Hadley Centre (HadCRUT4 en HadSST3) zelfs duidelijk groter is dan de onderlinge afwijking tussen diverse TSI en temperatuur data sets.
Dit impliceert dat de TSI data sets en de temperatuur data sets onderling niet gemakkelijk van elkaar te onderscheiden zijn. De interne consistentie tussen diverse combinaties van TSI en temperatuur data sets blijkt zelfs groter dan tussen de beide temperatuur data sets van het Hadley Centre en de NASA – waarbij vooral de GISS SST zich manifesteert als een data set met een opvallend grote afwijking t.o.v. de andere data sets.
Relevant is ook dat de LISIRD met 6 van de 7 overige data sets een correlatie toont die hoger is dan de correlatie van de gemiddelde waarden van de TSI data sets en de temperatuur data sets; ook bij deze vergelijking vormt de GISS SST de enige uitzondering waarbij dit niet het geval is. Opvallend is ook dat de correlatie tussen LISIRD TSI en de gemiddelde waarden van de 4 temperatuur data sets (0,962) hoger is dan de correlatie tussen de GISS SST en de gemiddelde waarden van de 4 temperatuur data sets (0,919).
Uit het totaalbeeld blijkt dat in tegenstelling tot de uitzonderingspositie van de GISS SST data set de bijbehorende GISSTEMP v4 data set voor de zeewateroppervlaktetemperatuur daarentegen wel relatief sterke correlaties toont met de vier TSI data sets (waarbij de correlatie waarden consequent het p=0,01 significantie niveau overtreffen). Kortom, de beide data sets voor de mondiale temperatuur tonen gezamenlijk een sterker patroon van correlaties met de TSI data sets dan het gemiddelde van de beide temperatuur data sets voor het zeewateroppervlak het geval is.
Het eerder beschreven profiel dat bij alle 8 data sets is aangetroffen kan voor de 4 temperatuur data sets nog nader worden gespecificeerd. Onderstaand overzicht toont o.a. dat vooral de temperatuurverschillen tussen de periodes rond het jaar 1912 en het jaar 1976 zeer gering zijn (deze twee periodes vormen tevens de meest recente bodemfases van de multi-decadale cyclus, zoals beschreven in het augustus 2019 artikel). De verschillen liggen binnen een bandbreedte van slechts 0,022 °C. Dit betekent dat de 4 temperatuur data sets min of meer dezelfde temperatuur stijging tonen tussen de periodes rond de jaren 1912 en 1976. Dit impliceert dat er sprake is van hoge consensus m.b.t. de omvang van de temperatuurstijging in de periode rond deze minima en dit blijkt van toepassing op zowel beide zeewateroppervlaktetemperatuur data sets als beide mondiale temperatuur data sets.
1890 (= 1889-1891): HadSST3 +0,215 °C; HadCRUT4 +0,163 °C; GISSTEMP v4 +0,160 °C; GISS SST +0,230 °C;
1912 (= 1911-1913): HadSST3 +0,0 °C; HadCRUT4 +0,0 °C; GISSTEMP v4 +0,0 °C; GISS SST +0,0 °C;
1933 (= 1934-1935): HadSST3 +0,298 °C; HadCRUT4 +0,288 °C; GISSTEMP v4 +0,193 °C; GISS SST +0,133 °C;
1954 (= 1953-1955): HadSST3 +0,440 °C; HadCRUT4 +0,394 °C; GISSTEMP v4 +0,320 °C; GISS SST +0,266 °C;
1976 (= 1975-1977): HadSST3 +0,374 °C; HadCRUT4 +0,354 °C; GISSTEMP v4 +0,360 °C; GISS SST +0,376 °C;
1996 (= 1953-1955): HadSST3 +0,711 °C; HadCRUT4 +0,767 °C; GISSTEMP v4 +0,800 °C; GISS SST +0,683 °C;
2017 (= 2016-2018): HadSST3 +1,029 °C; HadCRUT4 +1,158 °C; GISSTEMP v4 +1,316 °C; GISS SST +1,035 °C.
In de laatste paragraaf (X Discussie & conclusie) wordt op basis van de zonnegevoeligheid berekend dat de opwarming die tussen de 17de eeuw (op basis van het Maunder minimum) en de 3-jarige periode rond het jaar 1912 ongeveer 0,5 °C bedraagd. Dit impliceert dat de zeewateroppervlaktetemperatuur sinds de 17de eeuw in totaal met 1,5 °C is gestegen en voor de atmosfeer ligt de waarde iets 0,15-0,30 °C met een waarde van 1,65-1,80 °C.
Tenslotte wordt bij de procentuele stijging tussen de 3-jarige periodes rond de jaren 1996 en 2017 t.o.v. de stijging tussen de 3-jarige periodes rond de jaren 1976 en 1996 een opmerkelijk verschil aangetroffen. Want de beide data sets van het Hadley Centre tonen een kleine vertraging in de temperatuurstijging terwijl de beide data sets van de NASA een relatief groter versnelling tonen.
Overzicht van de procentuele verschillen tijdens het verloop van de laatste 2 zonnecycli:
– data sets Hadley Centre: HadSST3 -5,6%; HadCRUT4 -5,3%;
– data sets NASA: GISSTEMP v4 +17,3%; GISS SST +14,7%.
Deze procentuele verschillen beschrijven een fundamentele inconsistentie tussen de beide data sets van het Hadley Centre en de beide data sets van de NASA.
VIII – Satelliet tijdperk: ACRIM-PMOD controverse is cruciaal voor invloed van zon
 In paragraaf VI van het februari artikel is beschreven dat sinds de jaren ’90 sprake is van controverse over de invloed van de zon. Er is beschreven dat twee van de drie onderzoeksteams die sinds het begin van de satelliet metingen in 1978 direct verantwoordelijk zijn geweest voor alle facetten van TSI satellietmetingen, zich publiekelijk hebben gedistantieerd van de PMOD methodiek waarop het IPCC haar visie in AR5 heeft gebaseerd25-27.
In paragraaf VI van het februari artikel is beschreven dat sinds de jaren ’90 sprake is van controverse over de invloed van de zon. Er is beschreven dat twee van de drie onderzoeksteams die sinds het begin van de satelliet metingen in 1978 direct verantwoordelijk zijn geweest voor alle facetten van TSI satellietmetingen, zich publiekelijk hebben gedistantieerd van de PMOD methodiek waarop het IPCC haar visie in AR5 heeft gebaseerd25-27.
Dit vormt een cruciale kwestie want uit figuur 8.10 in AR59 (= figuur 12, zie afbeelding) blijkt dat alleen de PMOD een beeld beschrijft waarbij de TSI minima een negatieve trend tonen, terwijl zowel de ACRIM als ook de RIMB en de SORCE/TIM vanaf de jaren ’80 een positieve trend beschrijven voor de minima – met name wanneer rekening wordt gehouden met de 22-jarige magnetische cyclus van de zon. Overigens, de Belgische RIMB beschrijft (net als de LISIRD TSI data set) vanaf het minimum van de midden jaren ’80 een voortdurende stijging.
Het IPCC onderkent in AR5 weliswaar dat bij het bestuderen van lange termijn veranderingen in de activiteit van de zon de aandacht meestal is gericht op de minima omdat deze zowel een meer “stabiele” als een meer “relevante” indicator vormen voor de langetermijntrend dan de maxima9 Echter, het IPCC gebruikt vervolgens de volgende redenering om het belang van de minima alsnog geheel te negeren:
“To avoid trends caused by comparing different portions of the solar cycle, we analyze TSI changes using multi-year running means.”9
Van belang is ook dat het IPCC in haar beschrijvingen veelvuldig refereert aan de 11-jarige zonnecyclus; echter, de 22-jarige magnetische zonnecyclus is hierbij nooit ter sprake gebracht. In het verslag van de “expert review comments” bij het IPCC AR5 rapport (2013) is wel 1x door een expert reviewer terloops gerefereerd aan de 22-jarige cyclus, maar in haar reactie laat het IPCC zelf het onderwerp onbesproken28.
Naast de keuze van het IPCC om in haar analyse niet expliciet rekening te houden met het feit dat vooral de minima indicatief zijn voor de langetermijntrend van de totale zonnestraling, vormt ook het ontbreken van de 22-jarige magnetische zonnecyclus een fundamentele tekortkoming binnen het raamwerk van het IPCC. Want enkel op basis van de 22-jarige cyclus kan het belang van de primaire minima worden onderkend, wat ook van belang is met het oog op de impact van klimaatruis t.g.v. bijvoorbeeld de relatief grote fluctuaties in het UV spectrum van de zon (deze fluctuaties kunnen in de orde van 100x groter zijn dan de fluctuaties binnen het gehele spectrum29). Dit punt is bovendien ook relevant bij het bestuderen van de temperatuur impact van de aantasting van de ozonlaag, waarvan bekend is dat deze een cruciale rol speelt bij blokkeren van de voor de mens schadelijke UV zonnestraling.
In paragraaf VII van het februari artikel is een uitgebreide beschrijving gegeven voor de LISIRD data set. De LISIRD betreft weliswaar geen “officiële” TSI doch deze bevat in de ogen van LASP hoofdonderzoeker Greg Kopp (figuur 13) wel de beste waarden die beschikbaar zijn voor de experts; de data die betrekking heeft op het satelliet tijdperk is gebaseerd op de Community-Consensus TSI Composite30.
Figuur 13: LISIRD auteur Greg Kopp beschrijft de controverse onder TSI experts over invloed van de zon op klimaatverandering.
IX – Fysische onderbouwing voor invloed zon is conceptueel eenvoudiger dan de CO2-hypothese
Deze paragraaf presenteert een beschrijving van de natuurkundige mechanismen die betrokken zijn bij de invloed van respectievelijk de zon (IX-a) en CO2 (IX-b) op het klimaat.
• IX-a Het natuurkundig mechanisme achter de invloed van de zon op het klimaat
De zon staat bekend als de drijvende kracht achter alle klimaat en weersverschijnselen. Het mechanisme laat zich primair gemakkelijk duiden: de temperatuur op aarde volgt de totale zonnestraling tijdens de fase waarbij de primaire minima zich aandienen binnen het perspectief van de 22-jarige magnetische zonnecyclus. De 22-jarige zonnecyclus ontstaat uit een complex van korte en lange termijn cycli op basis van magnetische activiteit, welke bepalend is voor zowel de omvang als de samenstelling van de zonnestraling die de aarde bereikt.
De fase van de primaire minima vormt de meest stabiele en betrouwbare indicator voor de activiteit van de zon op de lange termijn. De minima ontstaan doordat de druk component in de energiegolven van de zon gepaard gaan met een lagere frequentie31 in combinatie met: een hogere amplitude + een groter aantal actieve regionen32. De maxima tonen het omgekeerde patroon: de frequentie is hoger maar de amplitude + het aantal actieve regionen is lager. Ook is bekend dat de samenstelling van de zonnestraling vooral bij de maxima grote fluctuaties toont; dit gaat zelfs gepaard met de vorming van twee maxima die zich verspreid over een periode van 2-3 jaar aandienen. Het eerste maximum wordt gekenmerkt door o.a. een hoog niveau van het verre UV + relatief veel kleine zonnevlekken + zonnevlammen; het tweede maximum wordt gekenmerkt door zowel grote zonnevlekken als grote zonnevlammen en aurora’s.
Dit verklaart waarom juist tijdens maxima relatief gemakkelijk ‘klimaatruis’ ontstaat; de atmosfeer van de aarde kan de minder krachtige hoogfrequente energie van de zon gemakkelijker reflecteren (via bijvoorbeeld Albedo) of absorberen (via bijvoorbeeld afbraak van UV straling in de ozonlaag). In het december artikel is aangetoond dat de correlatie tussen de TSI en de temperatuur bij de minima tot wel 4x hoger is dan bij de maxima het geval is.
UV zonnestraling vormt de primaire bron van energie voor de atmosfeer en speelt een centrale rol bij zowel de verticale, thermische en electronische structuur van de atmosfeer. Hierbij moet wel de kanttekening worden gemaakt dat het UV spectrum 8% van het totale zonnespectrum vormt aan de top van de atmosfeer, waarvan 3-5% overblijft bij het aardoppervlak. Bovendien speelt UV straling een cruciale rol binnen de ozon cyclus in de atmosfeer. Ook dit is van belang omdat ozon warmte genereert in de stratosfeer, zowel door de ultraviolette straling van de zon te absorberen in de hogere atmosfeer (stratosfeer) als door opgaande infraroodstraling uit de lagere atmosfeer (troposfeer) te absorberen.
De zon genereert via UV straling iedere dag opnieuw ongeveer 12% van alle ozon in de atmosfeer; de aantasting van de ozonlaag zorgt ervoor dat vooral meer van de hoog energetische UV-C en UV-B straling dieper kan doordringen in de atmosfeer. Van de 3 mogelijke factoren (UV, kosmische straling en/of zonnewind) die een rol kunnen spelen bij het ontstaan van de versterkende factor vormt UV een kandidaat die in potentie voor grote effecten kan zorgen in de circulatie van de atmosfeer; circulatie modellen suggereren dat de variaties relatief klein zijn. Wel duidt de afkoeling van de stratosfeer die sinds het begin van de jaren ’80 is ontstaan logischerwijs op een verticaal transport van energie vanuit de hogere atmosfeer naar de lagere atmosfeer, waarbij UV een sleutelrol speelt.
Relevant is ook dat zowel in het december artikel als het februari artikel patronen zijn beschreven waaruit blijkt dat de zon ook een duidelijke ‘footprint’ toont in de ENSO cyclus.
De wetenschappelijke literatuur beschrijft dat het temperatuurverschil tussen een passieve zon en een actieve zon in de orde van grootte ligt van 1 °C op basis van boringen in de aardkorst of de ijskappen33; Svensmark beschrijft hiervoor een iets hogere waarde: 1-2 °C34. Dit komt bij benadering overeen met de inschatting dat de zon sinds het Maunder minimum voor ongeveer 1,1 °C opwarming heeft gezorgd (zie paragraaf VI). Dit vereist een hoge versterkende factor want de fluctuaties in de TSI zijn energetisch bezien relatief klein. Echter, de energie van de zon bestaat niet alleen uit de fotonen die via de TSI worden gemeten. Want de energie van de zon bereikt ook via magnetisme en energetische deeltjes de aarde. Zowel de impact op het klimaat als het bijbehorende natuurkundige mechanisme van deze 2 bijkomstige factoren wordt niet meegenomen in de zienswijze van het IPCC. Overigens is pas in 2019 duidelijk geworden dat bijvoorbeeld de kracht van het magnetische veld van de zon tot zeer recent met een factor 10 te laag is ingeschat.
Overigens, de recente extreme omstandigheden bij de zon worden ook aangetroffen bij de activiteit van de zon in termen van het aantal zonnevlekken. In 2004 is door wetenschappers van het Max Planck instituut vastgesteld dat het aantal zonnevlekken in de 2de helft van de 20ste eeuw op een recordniveau is beland binnen het perspectief van de afgelopen 8.000 jaar35. In onderstaande video beschrijft Prof. Nir Shaviv de voortdurende invloed van de zon op het klimaat in het perspectief van de geschiedenis van de aarde.
VIDEO: DTU lezing door Prof. Nir Shaviv over de voortdurende rol van de zon in klimaatverandering;
vanaf 13:30 wordt in de video het perspectief besproken dat in de aanvullende sectie hieronder in figuur 14 wordt getoond.
Figuur 14: De zon heeft een groot temperatuur effect gedurende de 11-jarige zonnecyclus; de impact is 5-7 maal groter dan verwacht op basis van enkel de totale zonnestraling (TSI)34.
DE TSI TOONT ENKEL HET DIRECTE DEEL VAN DE ENERGIE VAN DE ZON
Conceptueel mag de verklaring voor de invloed van de zon op het eerste gezicht wellicht relatief eenvoudig lijken maar getalsmatig betreft vooral het aspect van de noodzakelijke versterkende factor een complexe materie. Getalsmatig is van belang dat slechts een deel van de zonnestraling gemeten aan de top van de atmosfeer het aardoppervlak bereikt en verwarmt. Rekening houdend met de bolvorm van de aarde + een albedo factor van 30-39% (percentages volgens Wikipedia) bereikt slechts 15,25-17,5% van de zonnestraling het aardoppervlak. Svensmark beschrijft voor de kracht van het zonnesignaal in het oceaan systeem tijdens de 11-jarige zonnevlekkencyclus een waarde van 0,2 W/m234 (zie figuur 14).
Energetisch bezien dient hiervoor noodzakelijkerwijs een versterkend mechanisme te bestaan. M.b.t. de versterking van het signaal van de zon denken diverse experts vooral aan een natuurlijk mechanisme via 3 mogelijke factoren: UV, kosmische straling en/of zonnewind. Svensmark als Shaviv beschrijven een (indirecte) versterkende factor voor het signaal van de 11-jarige zonnecyclus in het oceaan systeem, welke er voor zorgt dat de impact in de orde van 5 tot 7 maal groter is dan de TSI signaal zelf34,36. De beschrijving van Svensmark (zie ‘figure 16’ in figuur 14) impliceert dat binnen de 11-jarige zonnecyclus een TSI amplitude van 0,5 W/m2 (= 5x de waarde van 0,1 W/m2 aan het aardoppervlak) aan de top van de atmosfeer (TOA) gepaard gaat met een temperatuur amplitude van 0,05-0,08 °C.
De beschrijving van Svensmark impliceert een waarde van slechts 0,50-0,80 °C per W/m2 aan het aardoppervlak; terwijl de zonnegevoeligheid die in paragraaf III en paragraaf IV is beschreven voor de minima komt overeen met een waarde van 6,0 °C per W/m2 aan het aardoppervlak (op basis van dezelfde vermenigvuldigingsfactor van 5x die door Svensmark wordt gebruikt in combinatie met de waarde: 1,2 °C per W/m2). Dit betekent dat het lange termijn perspectief van de minima bij de temperatuur ontwikkeling een versterkende factor van 7,5 tot 12 vereist t.o.v. het perspectief van de zonnecyclus; dit komt overeen met een versterkende factor met een waarde van 37,5 tot 84 t.o.v. het TSI signaal in het oceaan systeem bij het aardoppervlak.
De omvang van deze getallen kunnen we begrijpen via het feit dat de fluctuaties voor de TSI als geheel relatief klein zijn met een variatie in de orde van 0,1%; echter, de omvang van de fluctuaties verschillen zeer sterk want voor het UV spectrum geldt dat de variatie in de orde van 10-20% van de totale TSI ligt – wat ongeveer een factor 100-200 hoger is t.o.v. het gehele zonnespectrum29. Svensmark beschrijft dat de fluctuaties bij een golflengte van 120-121 nm gepaard gaan met veranderingen in de orde van 40%, wat 400x hoger is dan de fluctuaties van het gehele TSI spectrum34. Bij extreem ultraviolete [EUV] frequenties komen variaties voor die kunnen oplopen tot in de orde van 6%, wat neerkomt op een factor 30 hoger t.o.v. de 0,02% die van toepassing is op zichtbaar licht. Fundamenteel is hierbij ook van belang dat EUV straling bestaat uit hoog energetische fotonen, welke in potentie een hoge impact kan hebben op de atmosfeer.
Uit UV proxies op basis van algen blijkt dat bij Antarctica de hoeveelheid UV straling aan het einde van de 20ste eeuw met ongeveer 50% verder is opgelopen t.o.v. de vorige pieken met waarden van minder dan 1,2 Tscy/TCC die halverwege het vorige millenium hebben plaatsgevonden. Dit resulteert in een hockeystick grafiek die nog steiler oploopt dan bij de zonnevlekken het geval is met waarden van bijna 1,8 Tscy/TCC37 (zie figuur 15).
Kortom, de dynamiek van de invloed van de zon is duidelijk zichtbaar maar getalsmatig is er sprake van een onbegrepen mechanisme. Dit komt vermoedelijk omdat de energie van de zon ontstaat op basis van een combinatie van een directe invloed van: (1) fotonen [UV], in combinatie met indirecte invloeden van: (2) energetische deeltjes [zonnewind] en (3) magnetische velden [kosmische straling].
Via de TSI meten we dus enkel de directe invloed van fotonen. De fluctuaties van de zon ontstaan op basis van magnetisme; dit maakt direct duidelijk dat de impact hiervan (in combinatie met de invloed van kosmische straling) logischerwijs in het perspectief van de kosmische constellaties minstens even groot kan zijn. Onderstaande citaat uit het werk van van Geel & Ziegler38 geeft hiervoor een indicatie:
“Measurements show that between 1964 and the 1990s the total magnetic flux leaving the Sun (solar wind) increased by a factor of 1.4 with surrogate measurements indicating that it increased since the Little Ice Age by 350%, while the GCR flux decreased by about 50% to reach a low in the 1990s.”
Figuur 15: Zowel zonnevlekken (onderste deel afbeelding) als UV proxies op basis van scytonemine pigment gevormd door bacteriën bij algen op Antarctica (bovenste deel afbeelding) tonen aan het einde van de 20ste eeuw zeer hoge niveaus (~1,8 Tscy/TCC) resulterend in een grafiek met de vorm van een ‘hockeystick’; hierbij is bij de UV proxies het verloop nog steiler dan bij de zonnevlekken het geval is37. De afname van ozon in de periode 1960-2000 van 350 UD naar 50 DU is weergegeven in een apart kader.
• IX-b Het natuurkundig mechanisme achter de invloed van de CO2 op het klimaat
Sinds het begin van de industriële revolutie is de concentratie van CO2 in de atmosfeer wereldwijd inmiddels met ongeveer de helft toegenomen van ongeveer 277 ppm rond het jaar 1700 tot waarden hoger dan 415 ppm halverwege april 2020. Dit betekent dat in 320 jaar tijd het percentage CO2 is toegenomen van bijna 3 deeltjes naar ruim 4 deeltje per 10.000 deeltjes in de atmosfeer.
De website van de NASA beschrijft dat de temperatuur impact van het totale broeikaseffect 33 °C bedraagd; wolken zorgen hierbij voor een afkoeling van netto -5 °C39. Volgens het IPCC komt de impact van wolken overeen met een stralingsforcering van -13 W/m240. Logischerwijs betekent dit dat alle broeikasgassen samen bij benadering verantwoordelijk zijn voor een temperatuur effect van 38 °C (zonder de impact van wolken). De veronderstelling is dat 9-26% van dit temperatuureffect ontstaat via CO2; dit impliceert een temperatuur effect voor CO2 in de orde van 3,42-9,88 °C (afgezien van een eventueel logaritmisch effect effect dat de impact zal drukken). Een toename van CO2 in de atmosfeer met 50% zou daarmee logischerwijs in de orde van -1,71-4,94 °C behoren te liggen volgens deze opvatting. Het IPCC verondersteld hierbij dat de opwarming sinds het begin van de industriële revolutie grotendeels aan broeikasgassen kan worden toegeschreven; AR5 beschrijft dat men het waarschijnlijk acht dat de temperatuurstijging sinds het begin van de industriële revolutie mogelijk zelfs geheel het gevolg is van broeikasgassen. Men redeneert hierbij dat het broeikaseffect van CO2 wordt versterkt door feedback systemen waarbij positieve feedback domineert; dit vormt tevens de verklaring waarom de temperatuur impact van de toename van CO2 hoger is dan de 1,1 °C die onder laboratorium omstandigheden voor een verdubbeling van CO2 is aangetroffen. Het IPCC spreekt al sinds de jaren ’90 over een ‘klimaatgevoeligheid’ met een waarschijnlijke bandbreedte van 1,5-4,5 °C, wat verwijst naar het temperatuur effect van een verdubbeling van CO2.
Echter, deze beschrijving berust vrijwel geheel op een theoretisch denkkader want pas in 2015 werd voor het eerst door onderzoekers een direct empirisch bewijs getoond voor het bestaan van het mechanisme binnen het klimaat systeem beschreven door de broeikastheorie20. Deze onderzoekers hebben beschreven dat CO2 enige invloed (~10% van de trend) heeft bij de ’terugstraling’ van lange golf straling (infraroodstraling) vanuit de atmosfeer.
Een fundamenteel probleem in deze zienswijze vormt het feit dat voor ieder deeltje CO2 in de atmosfeer ongeveer 625 deeltjes beschikbaar zijn van het meest dominante broeikasgas, namelijk: waterdamp [H2O]. M.a.w. naast de 4 CO2 deeltjes per 10.000 deeltjes in de atmosfeer bevinden zich ongeveer 2500 deeltjes waterdamp binnen het klimaat systeem. Bovendien wordt aan één molecuul CO2 en één molecuul waterdamp [H2O] bij benadering ongeveer dezelfde stralingsforcering toegeschreven. Logischerwijs kunnen we hieruit afleiden dat waterdamp in theorie op basis van de kwantiteit t.o.v. de overige broeikasgassen grotendeels (mogelijk ruim 99%) verantwoordelijk kan worden gehouden voor het broeikaseffect van 38 °C. Een bevestiging voor dit beeld vormt de omvang van het temperatuur effect van een verdubbeling van CO2 onder laboratorium omstandigheden want een temperatuurstijging van 1,1 °C impliceert een bijdrage van minder dan 3% t.o.v. het totale broeikaseffect van 38 °C (na verrekening voor de impact van wolken); ook dit percentage ligt beduidend lager dan de CO2 bijdrage van 9-26% binnen het raamwerk van het IPCC op basis van de broeikastheorie. De impact van CO2 t.o.v. de overige broeikasgassen (afgezien van de impact van waterdamp) wordt in AR5 ingeschat op ongeveer 70%; voor methaan denkt men aan een bijdrage van 4-9% en voor ozon denkt men aan een bijdrage van 3-7%. Deze laatste percentages zijn representatief voor de zogenaamde ‘consensus’.
De zienswijze die op basis van de kwantitatieve verhoudingen een lagere impact voor CO2 als broeikasgas beschrijft is consistent met o.a. de wet van Henry + het feit dat binnen de natuurlijke cycli CO2 de temperatuur volgt en dus niet andersom. De wet van Henry beschrijft dat de toename in de concentratie van CO2 in de atmosfeer deels het gevolg is van de temperatuurstijging van het zeewaterwateroppervlak. Experts hebben ingeschat dat de temperatuurstijging verantwoordelijk is voor ongeveer 15% van de stijging van CO2 sinds het begin van de industriële revolutie; bij een temperatuur stijging van 1 graad Celsius kan bij benadering ongeveer 3% minder CO2 kan worden opgelost in het oceaanwateroppervlak. Hieruit blijkt dat fundamenteel bezien logischerwijs een aanzienlijk deel van de stijging van CO2 het gevolg is van de temperatuurstijging en dus niet andersom. Bovendien blijkt uit de getalsmatige analyse in dit artikel dat voor de periode t/m de jaren ’80 er geen ruimte is voor een significante bijdrage van CO2 en voor de periode na de jaren ’80 blijkt de bijdrage van ozon in het broeikaseffect (via de aantasting van de ozonlaag) indirect aanzienlijk groter dan bij CO2 het geval is.
Kortom, zowel het perspectief van de zon als CO2 toont inconsistenties die betrekking hebben op de omvang van de verhoudingen. Bij de zon draait het hierbij vooral om een versterkende factor in de orde van 37,5 tot 84; binnen de broeikastheorie vormt de beschikbaarheid van gemiddeld 625 deeltjes waterdamp t.o.v. 1 deeltje CO2 in de atmosfeer een nog grotere verhouding. Beide factoren laten zich empirisch bezien in het klimaat systeem bijzonder lastig onderzoeken. Dit komt omdat waterdamp deeltjes binnen het klimaat systeem zich manifesteren in wisselende toestanden met een variabele impact. De resultaten onder laboratorium omstandigheden voor een verdubbeling van CO2 tonen aan dat de verhouding t.o.v. de veel grotere beschikbaarheid van waterdamp wel is te overbruggen.
Echter, enkel binnen het perspectief van de CO2 theorie worden fundamentele inconsistenties aangetroffen waaruit blijkt dat de impact van CO2 binnen het klimaat systeem aanzienlijk complexer is dan wat laboratorium omstandigheden beschrijven. Bovendien bestaat het klimaat systeem grotendeels uit negatieve feedback systemen. De inconsistenties m.b.t. CO2 (wet van Henry + het feit dat CO2 de temperatuur binnen de natuurlijke cycli) vormen een aanwijzing dat binnen het klimaat systeem negatieve feedback systemen dominant zijn, ook m.b.t. de impact van CO2. Binnen het denkkader van het IPCC veronderstelt men dat positieve feedback systemen verantwoordelijk zijn voor een versterkt broeikaseffect. Uit de PMOD-ACRIM controverse blijkt dat hierbij de rol van de zon is genihiliseerd. Dit gebeurt op basis van aannames en aanpassingen die door meerdere onderzoeksteams op het allerhoogste niveau inmiddels al ruim 2 decennia zijn herkend als een methode die niet representatief is voor wat de satelliet data daadwerkelijk beschrijft:
“Several TSI satellite composites have been proposed: ACRIM, PMOD, RMIB and those suggested by Scafetta and Dudok de Wit et al. Although these composites use different sets of TSI satellite records and merging methodologies, they are relatively equivalent since about 1992, the beginning of the ACRIM2 record, because they are all based on high-quality TSI observations. Yet, as clarified below, PMOD used their own modified versions of the original results compiled by the experiment teams for the SMM/ACRIM1, UARS/ACRIM2 and Nimbus7/ERB records to cover the period 1978-1992 and, therefore, its proposed record cannot be considered a real TSI satellite composite but a model construction. The ACRIM-PMOD controversy is about the scientific legitimacy of such modifications.“41
X – Discussie & conclusie
In dit artikel is aangetoond op basis van 3-jarige periodes rond de minima van de zonnecyclus dat 93% van de variantie in het temperatuurverloop van het zeewateroppervlak [HadSST3] tussen het laatste decennium van de 19de eeuw en de midden jaren ’80 wordt verklaard door de totale zonnestraling [LISIRD]. Hierbij is gebruik gemaakt van een correctie gericht op de secundaire minima. Voor de gehele periode vanaf het minimum rond 1890 wordt 96% van de variantie over verklaard door de combinatie van de totale zonnestraling en de afname van ozon concentraties.
Tevens is aangetoond dat zowel CO2, AOD en ENSO cyclus in beide periodes geen meerwaarde genereren in termen van de verklaarde variantie. Dit impliceert dat het sterke statistische verband tussen CO2 en de temperatuur berust op een spurieus schijnverband dat t/m de midden jaren ’80 geheel wordt verklaard door de zon. Bij de overgang tussen de minima rond de jaren 1985 en 1996 heeft het ontstaan van de ozonproblematiek dit schijnverband tijdelijk ondersteund. De aantasting van de ozonlaag is ontstaan onder invloed van het gebruik van de kunstmatige CFK’s (niet t.g.v. de qua oorsprong natuurlijke CO2) en heeft tot gevolg gehad dat meer UV zonnestraling het aardoppervlak heeft kunnen bereiken. Tijdens de overgang tussen de minima rond de jaren 1985 en 1996 toonde de totale zonnestraling ondertussen een lichte daling maar nadien volgde tussen zowel 1996 en 2008 als tussen 2008 en 2017 een versnelling in de toename van de totale zonnestraling.
Het schijnverband tussen CO2 en de temperatuur manifesteert zich in het perspectief van zowel de primaire en secundaire minima, als ook bij de combinatie van beide minima series. Enkel de correlaties tussen zeewateroppervlaktetemperatuur en totale zonnestraling tonen een stabiel verband voor zowel de periode voorafgaand aan de ozonproblematiek als de gehele periode sinds 1880. Na een correctie gericht op de secundaire minima (+0,123 W/m2) blijkt de omvang van de correlatie tussen zeewateroppervlaktetemperatuur en TSI op basis van het 3-jarig gemiddelde voor beide periodes hoger dan de correlatie tussen de zeewateroppervlaktetemperatuur en CO2.
Het verband tussen de TSI [TOA] en de zeewateroppervlaktetemperatuur gaat gepaard met een zonnegevoeligheid van 1,2 °C per W/m2 voor het 3-jaren gemiddelde rond de primaire minima (+ de secundaire minima na toepassing van de correctie). Dit verband verklaart o.a. de gehele opwarming tussen de 3-jarige periodes rond de primaire zonneminima jaren 1996 en 2017. Tevens impliceert dit verband dat de zon verantwoordelijk is geweest voor ongeveer 1,1 °C van de opwarming die sinds het Maunder minimum aan het einde van de 17de eeuw is ontstaan op basis van een tussentijdse toename van de TSI met een waarde van 0,941 W/m2 t/m het zonneminimum jaar 2017.
In paragraaf VI van het december artikel is op basis van de PAGES 2k proxies een temperatuur trend beschreven van +0,0316°C per decennium voor de periode 1810-1902. Omdat het jaar 1902 een secundair minimum betreft en het jaar 1810 een primair minimum betreft (hierbij is rekening gehouden met de opeenvolging van 2 primaire minima op rij in de eerste decennia van de 18de eeuw) ligt het voor de hand om ook hierbij de correctie gericht op de secundaire minima toe te passen om een vergelijking met de PAGES 2k proxies mogelijk te maken. Het 3-jarig TSI gemiddelde rond de jaren 1810 en 1902 levert een stijging op van 0,052 W/m2; in combinatie met de correctie gericht op de secundaire minima (+0,123 W/m2) wordt een totale stijging gevonden van +0,175 W/m2 welke via de zonnegevoeligheid van 1,2 °C per W/m2 resulteert in een waarde van +0,21 °C. Het berekende temperatuurverschil op basis van de zon ligt daarmee voor de periode 1810-1902 dus ongeveer 0,1 °C lager dan de temperatuur trend die voor dezelfde periode op basis van de PAGES 2k proxies is gevonden.
Op dezelfde wijze is een berekening gemaakt voor de opwarming tussen het Maunder minimum en de 3-jarige periode rond het jaar 1810. De PAGES 2k proxies tonen een beeld waarbij de temperatuur rond het einde van het Maunder minimum een nog iets lager niveau heeft bereikt dan rond het jaar 1810. Op basis van de totale zonnestraling toont de opwarming tussen het Maunder minimum en de 3-jarige periode rond het jaar 1810 een omvang van 0,40 °C; opgeteld levert dit voor de periode tussen het Maunder minimum en de 3-jarige periode rond het jaar 1902 een temperatuurstijging van in totaal 0,61°C.
Een controle berekening voor het temperatuur verschil tussen het Maunder minimum en de 3-jarige periode rond het primaire minimum jaar 1912 (welke in paragraaf VII een stabiel referentiepunt heeft opgeleverd t.o.v. de periode rond het jaar 1976) levert een temperatuurstijging op van 0,51°C. Deze uitkomsten tonen een consistent beeld waarbij zowel de PAGES 2k proxies als de TSI een kleine temperatuurstijging beschrijft voor zowel de 18de eeuw als de 19de eeuw. In combinatie met het overzicht in paragraaf VI betreffende de temperatuurontwikkeling t.o.v. het jaar 1912 is hieruit af te leiden dat sinds het Maunder minimum de opwarming van de zeewateroppervlaktetemperatuur ruim 1,5 °C bedraagt. De mondiale temperatuur is ondertussen ongeveer 0,15-0,30 °C harder gestegen t.o.v. het zeewateroppervlak, met een waarde in de orde van ruim 1,65 °C op basis van de HadCRUT4 data set en hooguit 1,80 °C op basis van de GISSTEMP v4 data set.
I.v.m. de impact van faseverschillen tussen de zon en het oceaan systeem (de impact van de ENSO cyclus is vertraagd in de orde van 6 maanden) levert de data op basis van 3-jarige periodes rond de zonneminima logischerwijs waarschijnlijk zowel een meer stabiel als ook een meer betrouwbaar beeld op t.o.v. data op basis van de individuele zonneminima jaren. De impact van ‘klimaatruis’ (b)lijkt hierbij gereduceerd tot een ogenschijnlijk zeer laag niveau. De eerste 2 decennia van de 21ste eeuw werden bovendien gekenmerkt door laag niveau van vulkanisme; ook dit kan in potentie een (klein) deel van de temperatuurstijging verklaren sinds de 17de eeuw; doch logischerwijs gaat het hierbij om niet meer dan enkele honderdsten van een graad Celsius.
Aanvullend blijkt in het perspectief van de HadSST3 55% van de opwarming tussen de 3-jarige periodes rond de zonneminimum jaren 1976 en 2017 verklaart door de zon, zoals weergegeven in figuur 10B. De ozonproblematiek heeft ervoor gezorgd dat meer zonnestraling het aardoppervlak heeft kunnen bereiken; dit verklaart grotendeels de rest van de tussentijdse opwarming gedurende deze periode.
In de wetenschappelijke literatuur zijn afgelopen jaren inmiddels meerdere claims gepresenteerd door onderzoekers die via fundamenteel andere onderzoeksbenaderingen ook hebben geconcludeerd dat de CFK’s een tijdelijke doch zeer significante impact hebben gehad bij het ontstaan van de relatief snelle opwarming sinds de jaren ’70. In 2013 werd door Prof. Qing-Bin Lu van de Universiteit van Waterloo (Canada) geclaimd dat CFK’s in combinatie met kosmische straling (onder invloed van het magnetische veld van de zon) de oorzaak zijn van de opwarming sinds 185042. En in januari 2020 is door een groep van onderzoekers uit de VS, Canada en Zwitserland beschreven dat CFK’s in de periode tussen 1955 en 2005 ongeveer 1/3 van de wereldwijde opwarming verklaren + ongeveer de helft van de opwarming bij de noordpool43. Geofysicus Peter Langdon Ward heeft vanaf 2009 onderzoek gepresenteerd waarin de rol van ozon in het klimaat centraal staat.
Op basis van 4 TSI data sets + 4 temperatuur data sets is aangetoond dat alle data sets bij het 3-jarige gemiddelde rond de primaire minima voor de periode 1890 t/m 1976 hetzelfde kenmerkende patroon tonen. De laagste waarde binnen dit patroon manifesteert zich altijd bij het 3-jarig gemiddelde rond het minimum van 1912; de jaren 1890 en 1933 tonen duidelijk hogere waarden en bij 1954 als 1976 worden nog hogere waarden aangetroffen. Van belang is dat de 4 TSI data sets niet duidelijk verschillen van de 4 temperatuur data sets; de variantie binnen beide groepen data sets blijkt duidelijk groter dan tussen de beide groepen data sets. De beide groepen data sets tonen op basis van de gemiddelde waarden een correlatie met een waarde van 0,928 [p=0,000].
Zowel bij 2 van de 4 van de TSI data sets (LISIRD & IPCC AR5) als bij de beide temperatuur data sets van het Hadley Centre (HadSST3 en HadCRUT4) tonen de 5 minima waarden op basis van het 3-jarig gemiddelde exact dezelfde volgorde. De meest wijkende data set betreft de GISS SST data set.
Opvallend is ook dat in het perspectief van de primaire minima beide data sets van het Hadley Centre een kleine vertraging tonen in de temperatuurontwikkeling tijdens de laatste twee volledige zonnecycli (1976-1996 en 1996-2017) terwijl de beide data sets van de NASA tijdens deze periodes een relatief grote versnelling tonen.
De hoogste correlatie die in dit perspectief is aangetroffen bij een combinatie van een TSI data set en een temperatuur data set betreft het koppel dat centraal staat in dit onderzoek, namelijk: de combinatie van de LISIRD en de HadSST3.
Ook is een beschrijving gepresenteerd voor het natuurkundige mechanisme dat de invloed van de zon op het klimaat verklaard. De wetenschappelijke literatuur presenteert gedetailleerde beschrijvingen waarin op basis van o.a. een drietal kandidaat factoren (UV, kosmische straling en/of zonnewind) het ontstaan van het noodzakelijke versterkend mechanisme dat nodig is om het temperatuureffect te verklaren dat wordt aangetroffen bij de 11-jarige zonnecyclus. In dit onderzoek is duidelijk geworden dat een nog groter versterkend mechanisme werkzaam is bij het verloop van de minima tussen de 3-jarige periodes rond het jaar 1890 en jaar 2017 – welke betrekking hebben op een periode van in totaal 130 jaar.
Dit onderzoek heeft enkele cruciale tekortkomingen in het denkkader van het IPCC onder de aandacht gebracht. Deze tekortkomingen reiken enerzijds een verklaring voor hoe het vermeende “onbegrepen” verband44 tussen de activiteit van de zon en het klimaat op aarde is ontstaan en anderzijds vormen ze handvatten om de relatie tussen beide factoren beter te kunnen doorgronden:
• 1 – Het IPCC houdt in haar analyse geen rekening met de 22-jarige magnetische zonnecyclus
• 2 – Het IPCC houdt in haar analyse onvoldoende rekening met de relevantie van de zonneminima
• 3 – Het IPCC baseert in AR5 haar conclusie m.b.t. de zon op de PMOD data set, terwijl diverse TSI expert teams de PMOD als niet-representatief beschouwen voor de satellietmetingen
• 4 – Het IPCC veronderstelt dat het temperatuureffect van de 11-jarige zonnevlekkencyclus slechts 0,06 °C bedraagd (op basis van CMIP5 klimaatmodellen); Wikipedia beschrijft op basis van Camp & Tung (2007) dat rekening mag worden gehouden met een impact die 2x tot mogelijk zelfs 4x hoger is, namelijk: 0,18 +/- 0,06 °C45
• 5 – Het IPCC houdt geen rekening met het feit dat binnen de natuurlijke cycli CO2 de temperatuur volgt en dus niet andersom
• 6 – Het IPCC houdt geen rekening met de wet van Henry (~15% van de CO2 stijging is het gevolg van de temperatuurstijging; dit resulteert in een theoretische inconsistentie m.b.t. de theorie die veronderstelt dat CO2 voor een groot deel verantwoordelijk is voor de temperatuurstijging sinds 1850)
• 7 – Het IPCC houdt m.b.t. de lange termijn trends geen rekening met een fundamenteel verschil voor en na het ontstaan van de ozonproblematiek (+ het ontstaan van de inverse relatie tussen de temperatuurontwikkeling in de lagere en hogere atmosfeer)
• 8 – Het IPCC legt teveel nadruk op korte termijn trends: bij het vaststellen van recente trends op mondiaal niveau dient men rekening te houden met de invloed van de multi-decadale natuurlijke cyclus (op mondiaal niveau ontstaat deze vooral t.g.v. de zon, lokaal kunnen cycli binnen het oceaan systeem hierbij ook een rol spelen).
Bovenstaande punten vormen een beeld dat aantoont dat het IPCC een onevenwichtig incompleet beeld beschrijft waarbij de rol van de zon structureel wordt genihiliseerd in combinatie met de neiging om op lichtzinnige wijze veranderingen binnen het klimaat systeem toe te schrijven aan antropogene invloeden. De inconsistenties aangaande het statistische verband tussen de temperatuurontwikkeling en CO2 worden hierbij structureel genegeerd. Illustratief hiervoor is het onderzoek waaruit blijkt dat pas in 2015 onderzoekers hebben gemeld voor het eerst enig empirisch bewijs te hebben gevonden voor het bestaan van enige invloed van CO2 op de impact van de straling van de atmosfeer (~10% van de trend); dit gebeurde op basis van data over een tijdspanne van slechts één 11-jarige periode20.
De inverse relatie tussen de temperatuurontwikkeling in de lagere atmosfeer (troposfeer) en de hogere atmosfeer (stratosfeer) is pas in de begin jaren ’80 ontstaan; dit valt samen met de periode waarin de aantasting van de ozonlaag is ontstaan. Het IPCC veronderstelt dat CO2 hiervoor verantwoordelijk kan worden gehouden. Tegelijkertijd stelt het IPCC bij haar modellen geen eisen m.b.t. consistente trends voor de periodes voor en na het ontstaan van deze inverse relatie. In dit onderzoek is beschreven dat de totale zonnestraling rondom de minima consistente correlaties toont met de temperatuur ontwikkeling voor vrijwel alle periodes vanaf het jaar 1880, met uitzondering van de overgang tussen de minima rond de jaren 1985 en 1996 – tijdens deze periode bereikte de ozonconcentratie het laagste niveau met een absoluut dieptepunt in het jaar 1994. Dit impliceert overigens niet dat de sterke relatie tussen zich beperkt tot de minima, want er zijn verschillende onderzoeksbenaderingen bekend waarmee de sterke relatie tussen zon en temperatuur kan worden aangetoond46.
M.b.t. de toekomst mag op basis van bovenstaande analyse logischerwijs worden geconcludeerd dat de temperatuurontwikkeling grotendeels zal worden bepaald door enerzijds de zon en anderzijds de invloed van de mens op de ozonlaag. Uitgaande van de afname van het impuls-moment in de beweging van de zon rond het baricentrum (en daarmee zeer waarschijnlijk ook de kracht van de zon) mag rekening worden gehouden met een temperatuur impact in de orde van -0,1 °C voor komende 3 decennia – conform de beschrijving in het werk van Scafetta beschreven in het december artikel. Daarnaast mag op basis van het te verwachten herstel van de ozonlaag dat voor komende 3 decennia ook in de planning zit, rekening worden gehouden met de mogelijkheid van een impact in de orde van -0,2 °C voor komende 3 decennia. De impact van het niet verklaarde deel van de temperatuurstijging (0,1 °C voor de zeewateroppervlakte temperatuur) is gering omdat hierin ook de impact zit t.g.v. de afname van vulkanisme naar een historisch laag niveau – in de toekomst vulkanisme nauwelijks nog verder afnemen. Logischerwijs kunnen beide effecten samen in potentie dus gaan zorgen voor een temperatuur impact van -0,3 °C in aanloop naar het jaar 2050. Dit sluit aan op de daling van enkele honderdsten van een graad Celsius die in de aanvullende bijlage in het artikel van juni 2019 reeds werd voorzien op basis van een analyse gericht op de multi-decennium klimaat cyclus; overigens, hierbij ontbrak indertijd nog het besef dat de zon verantwoordelijk is voor het ontstaan van deze klimaat cyclus.
Samenvatting in een notendop: de temperatuur volgde de totale zonnestraling (TSI) tijdens de minima t/m halverwege de jaren ’80; vervolgens heeft de aantasting van de ozonlaag vooral in de periode tussen 1984-86 en 1995-97 deze relatie verstoord.
* Tenslotte een woord van dank gericht aan André Bijkerk voor zijn adviezen van redactionele aard bij de serie van 5 artikelen (allen gewijd aan de invloed van natuurlijke cycli op het klimaat) die sinds juni 2019 is gepresenteerd; André schreef eerder zelf enkele artikelen over de invloed van de zon via het wolkendek (dit onderwerp wordt ook besproken in de video presentatie van Prof. Shaviv in paragraaf IX-a), zie: HIER en HIER.
Figuur A: zonnevlam die ontstaat op basis van magnetische activiteit van de zon.
VIDEO: NASA beschrijft de zonnecyclus.
De zonnecyclus gaat gepaard met een kosmische beweging van de zon rond het barycentrum;
in de bijlage van het december artikel is het mechanisme in detail beschreven.
Referenties:
1 – Artikel in Volkskrant: Warmt CO2 het klimaat echt wel op? (en nog drie knellende vragen die klimaatsceptici vaak stellen) (8 feb 2020).
2 – Artikel in Trouw: De zon is de meest nabije ster, maar we begrijpen er nog niet veel van (15 dec 2019).
3 – The Sun and the Earth’s Climate: Solar signals in surface climate – J.D. Haigh (oktober 2007).
4 – Met Office Hadley Centre observations datasets: HadSST3.1.1.0 Data [annual globe] (2019).
5 – LISIRD – Historical Total Solar Irradiance Reconstruction, Time Series (2018); auteur: Greg Kopp is de hoofdonderzoek van het SORCE/TIM project van het LASP (biografie).
6 – NASA: Stratospheric Aerosol Optical Thickness.
7 – Ensembloe Oceanic Nino Index (ENS ONI).
8 – Ozone Hole Area – NASA.
9 – IPCC, 2013: Climate Change 2013: The Physical Science Basis – 8 Anthropogenic and Natural Radiative Forcing – pagina 689 (hoofdstuk 8): “The year 1750, which is used as the preindustrial reference for estimating RF, corresponds to a maximum of the 11-year SC. Trend analysis are usually performed over the minima of the solar cycles that are more stable. … Maxima to maxima RF give a higher estimate than minima to minima RF, but the latter is more relevant for changes in solar activity.”
10 – 2018 Continues Record Global Ocean Warming – L. Cheng et al. (maart 2019) – Quote: “The vast majority of global warming heat ends up deposited in the world’s oceans, and ocean heat content (OHC) change is one of the best – if not the best – metric for climate change (Cheng et al., 2019)”.
11 – WMO: Key Climate Change Indicators from the Ocean (2017 update).
12 – Copernicus (EU): ‘INSIGHTS INTO THE ROLE OF THE OCEANS IN THE EARTH ENERGY BUDGET’ – K. von Schuckman (november 2017) – Citaat sheet 10: “The Earth energy imbalance can best be estimated from changes in ocean heat content, complemented by radiation measurements from space (von Schuckmann et al., 2016, NCC)”.
13 – The unstable CO2 feedback cycle on ocean planets – D. Kitzmann et al. (augustus 2015).
14 – Greenhouse gas growth rates – J. Hansen & M. Sato (september 2004); bron beschrijft 14% voor periode 1850-2003, aangepast voor 1850-2018 stijgt percentage naar 15%.
15 – Met Office Hadley Centre observations datasets: HadCRUT4 Data: download [global (NH+SH)/2] (2019)
16 – The Gnevyshev-Ohl Rule and Its Violations – N.V. Zolotova (februari 2015).
17 – Gnevyshev-Ohl rule for strong solar proton events – M. Ogurtsov & M. Londholm (maart 2016).
18 – The Gnevyshev-Ohl Rule for Physical Parameters of the Solar Magnetic Field: The 400-Year Interval – Yu.A. Nagovitsyn et. al. (oktober 2008).
19 – IPCC, 2013: Figure SPM.5
20 – Observational determination of surface radiative forcing by CO2 from 2000 to 2010 – D.R. Feldman, et al. (2015).
21 – Seasonal and Diurnal CO2 Patterns at Diekirch, LU 2003 – 2005 – F. Massen et al. (maart 2007); sectie 4.1 & 4.3.
22 – Breakpoint lead-lag analysis of the last deglacial climate change and atmospheric CO2 concentration on global and hemispheric scales – Zhi Liu et al. (mei 2018).
23 – Stratospheric ozone concentration – H. Ritchie & M. Roser (juni 2018).
24 – Oscillations of the baseline of solar magnetic field and solar irradiance on a millennial timescale – V. Zharkova, et al. (juni 2019).
25 – Astronomy and the Climate Crisis – A. Cooke (januari 2012); pagina 116-119.
26 – ACRIM3 and the Total Solar Irradiance database – R.C. Willson (februari 2014).
27 – Modeling Quiet Solar Luminosity Variability from TSI Satellite Measurements and Proxy Models during 1980-2018 – N. Scafetta, et al. (november 2019).
28 – Expert Review Comments on the IPCC WGI AR5 First Order Draft — Chapter 8 (2013) – comment 8-745.
29 – A solar irradiance climate data record – O. Coddington et al. (juli 2016).
30 – Solar Irradiance Variability: Comparisons of Models and Measurements – O. Coddington et al. (december 2019); figuur 6a.
31 – Background solar irradiance spectrum at high and low phases of the solar activity cycle – V. Ramió et al. (september 2002).
32 – Solar p modes in 10 years of the IRIS network – D. Salabert et al. (2004)
33 – The Role of the Solar Forcing in the 20th century climate change – N.J. Shaviv (2012)
34 – FORCE MAJEURE The Sun’s Role in Climate Change – H. Svensmark (2019).
35 – Max Planck Institute: The Sun is more active now than over the last 8000 years (2004)
36 – Using the oceans as a calorimeter to quantify the solar radiative forcing – N. Shaviv (2008).
37 – An 800-year ultraviolet radiation record inferred from sedimentary pigments in the Ross Sea area, East Antarctica (juli 2015)
38 – IPCC underestimate the sun’s role in climate change – B. van Geel & P.A. Ziegler (2013)
39 – NASA – ISCCP: International Satellite Cloud Climatology Project (2008); citaat: “The net effect of clouds on the climate today is to cool the surface by about 5°C (9°F).”.
40 – IPCC First Assessment Report.1990. UK: Cambridge University Press.table 3.1 (1990); citaat: “Clouds increase the global reflection of solar radiation from 15% to 30%, reducing the amount of solar radiation absorbed by the Earth by about 44 W/m2. This cooling is offset somewhat by the greenhouse effect of clouds which reduces the outgoing longwave radiation by about 31 W/m2. Thus the net cloud forcing of the radiation budget is a loss of about 13 W/m2.”.
41 – Modeling Quiet Solar Luminosity Variability from TSI Satellite Measurements and Proxy Models during 1980-2018 – N. Scafetta, et al. (november 2019).
42 – Cosmic-Ray-Driven Reaction and Greenhouse Effect of Halogenated Molecules: Culprits for Atmospheric Ozone Depletion and Global Climate Change – Q.-B. Lu (mei 2013).
43 – Substantial twentieth-century Arctic warming caused by ozone-depleting substances – L.-M. Polvani et al. (januari 2020).
44 – Klimaat brochure ‘Klimaatverandering, Wetenschap en Debat’ – Koninklijke Nederlandse Academie van Wetenschappen (2011).
45 – Surface warming by the solar cycle as revealed by the composite mean difference projection – C.D. Camp & K. Kit Tung (juli 2007).
46 – Re-evaluating the role of solar variability on Northern Hemisphere temperature trends since the 19th century – W. Soon et al. (augustus 2015).
KLIMAAT INDEX:
• Sinds 17de eeuw: +1,1 °C door zon
• SAMENVATTING: Hoe ontstaat de Klimaatcyclus en wat is haar impact?
• 1890-1976: Zon toont perfecte correlatie met temperatuur
• Zon verklaart opwarming sinds 1976
• El Nino & 66-jarige cyclus: CO2 overschat
• 70-Jarige cyclus: opwarming overschat
• Global warming vs fluctuaties in 2 dagen
• Oceaan: diepzee koelt af
• KlimaatCyclus.nl
Wat vertellen klimaat proxy indicatoren?
• PAGES 2k Network illustratie (2013)
• PAGES 2k Network illustratie: 2019 hockeystick grafiek vs 2013 temperatuur data
Bron hier.

![Zon opwarming temperatuur data sets temperatuur zonnestraling. (TSI) tijdens de minima t/m halverwege de jaren '80; vervolgens heeft de aantasting ozonlaag Figuur 1: CO2 toont een sterke correlatie (r = 0,942 [p=0,000]) met de GISS temperatuur data set; de omvang van de correlatie zegt echter niets over het oorzakelijke verband.](http://klimaatcyclus.nl/klimaat/pics/Oldenborgh-GISS-temperature-CO2-1880-2018-minima.jpg)
![Zon opwarming temperatuur data sets temperatuur zonnestraling. (TSI) tijdens de minima t/m halverwege de jaren '80; vervolgens heeft de aantasting ozonlaag Figuur 2: CO2 toont ook een sterke correlatie met de HadCRUT4 temperatuur data set (r = 0,918 [p=0,000].](http://klimaatcyclus.nl/klimaat/pics/solar-minimum-years-follow-HadCRUT4-global-temperature-CO2-correlation.jpg)
![Zon opwarming temperatuur data sets temperatuur zonnestraling. (TSI) tijdens de minima t/m halverwege de jaren '80; vervolgens heeft de aantasting ozonlaag Figuur 3: CO2 toont ook een sterke correlatie met de HadSST3 temperatuur data set (r = 0,878 [p=0,000]).](http://klimaatcyclus.nl/klimaat/pics/solar-minimum-years-follow-HadSST3-sea-surface-temperature-CO2-correlation.jpg)

![Zon opwarming temperatuur data sets temperatuur zonnestraling. (TSI) tijdens de minima t/m halverwege de jaren '80; vervolgens heeft de aantasting ozonlaag Figuur 5: Bij de 21 jaren rond de primaire zonneminima voor de periode vanaf het jaar 1880 toont de zeewateroppervlaktetemperatuur [HadSST3] met CO2 een correlatie waarde van 0,916 [p=0,000] van vergelijkbare omvang t.o.v. de correlatie waarde van 0,902 [p=0,000] voor de combinatie van zeewateroppervlaktetemperatuur en TSI [LISIRD].](http://klimaatcyclus.nl/klimaat/pics/solar-activity-temperature-CO2-correlation-primary-minima.jpg)
![Zon opwarming temperatuur data sets temperatuur zonnestraling. (TSI) tijdens de minima t/m halverwege de jaren '80; vervolgens heeft de aantasting ozonlaag Figuur 6: Bij de 19 jaren rond de primaire zonneminima vanaf het jaar 1880 toont de zeewateroppervlaktetemperatuur [HadSST3] een correlatie met dezelfde omvang t.o.v. CO2 (0,832 [p=0,000]) en de TSI (0,832 [p=0,000]).](http://klimaatcyclus.nl/klimaat/pics/solar-activity-temperature-CO2-correlation-secondary-minima.jpg)
![Zon opwarming temperatuur data sets temperatuur zonnestraling. (TSI) tijdens de minima t/m halverwege de jaren '80; vervolgens heeft de aantasting ozonlaag Figuur 7: Bij de 40 jaren rond de zonneminima voor de periode vanaf het jaar 1880 toont de zeewateroppervlaktetemperatuur [HadSST3] een correlatie in dezelfde orde van grootte t.o.v. zowel CO2 (r = 0,885 [p=0,000]) als de TSI (r = 0,841 [p=0,000]).](http://klimaatcyclus.nl/klimaat/pics/solar-activity-temperature-CO2-correlation-minima.jpg)
![Zon opwarming temperatuur data sets temperatuur zonnestraling. (TSI) tijdens de minima t/m halverwege de jaren '80; vervolgens heeft de aantasting ozonlaag Figuur 8: Na verhoging van de secundaire minima met 0,123 W/m2 blijkt voor de periode t/m de jaren '70 de correlatie tussen zeewateroppervlaktetemperatuur en TSI bij de combinatie van de beide minima series hersteld tot een waarde van 0,813 [p=0,000]; deze gecorrigeerde correlatie waarde komt exact overeen met de waarde bij de primaire minima (0,813 [p=0,000]) en de afwijking is bovendien zeer gering t.o.v. de waarde bij de secundaire minima (0,808 [p=0,000]).](http://klimaatcyclus.nl/klimaat/pics/solar-activity-temperature-CO2-correlation-minima-with-secundary-adjusted.jpg)

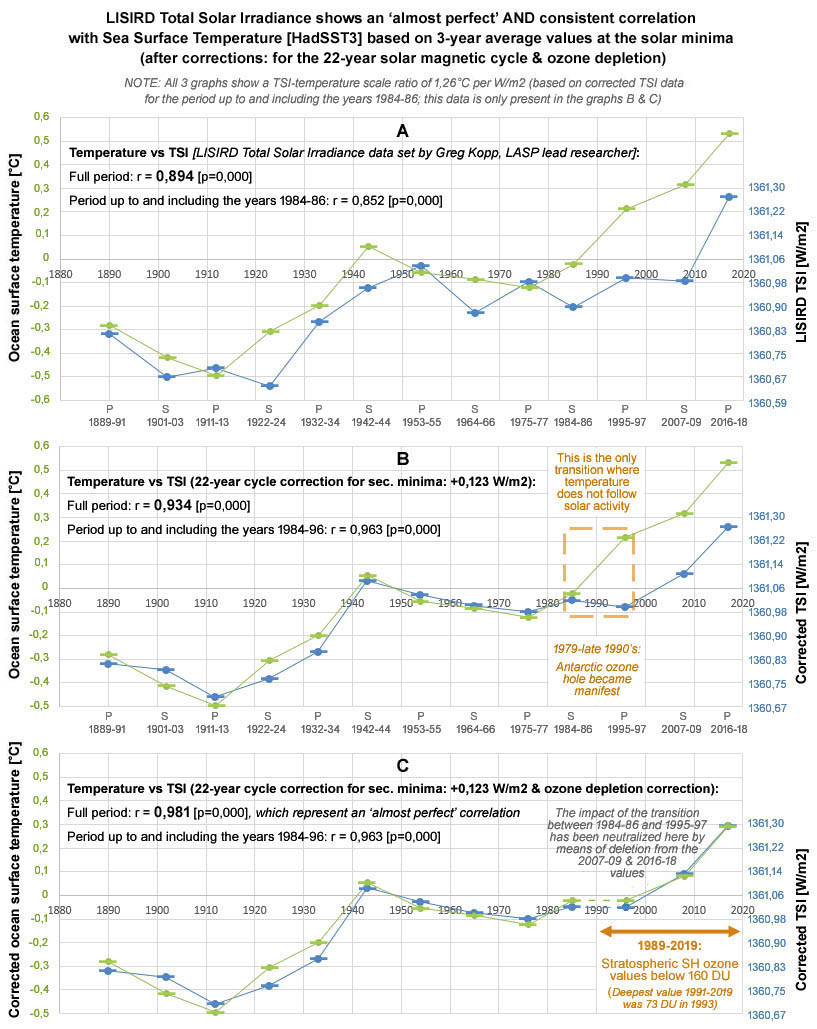
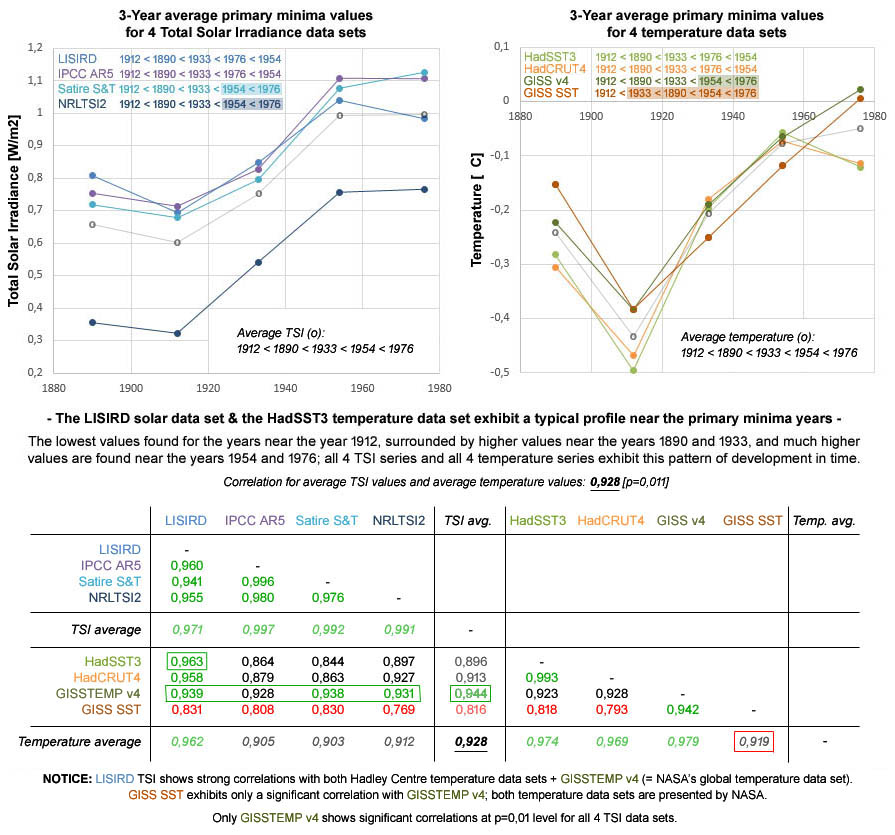
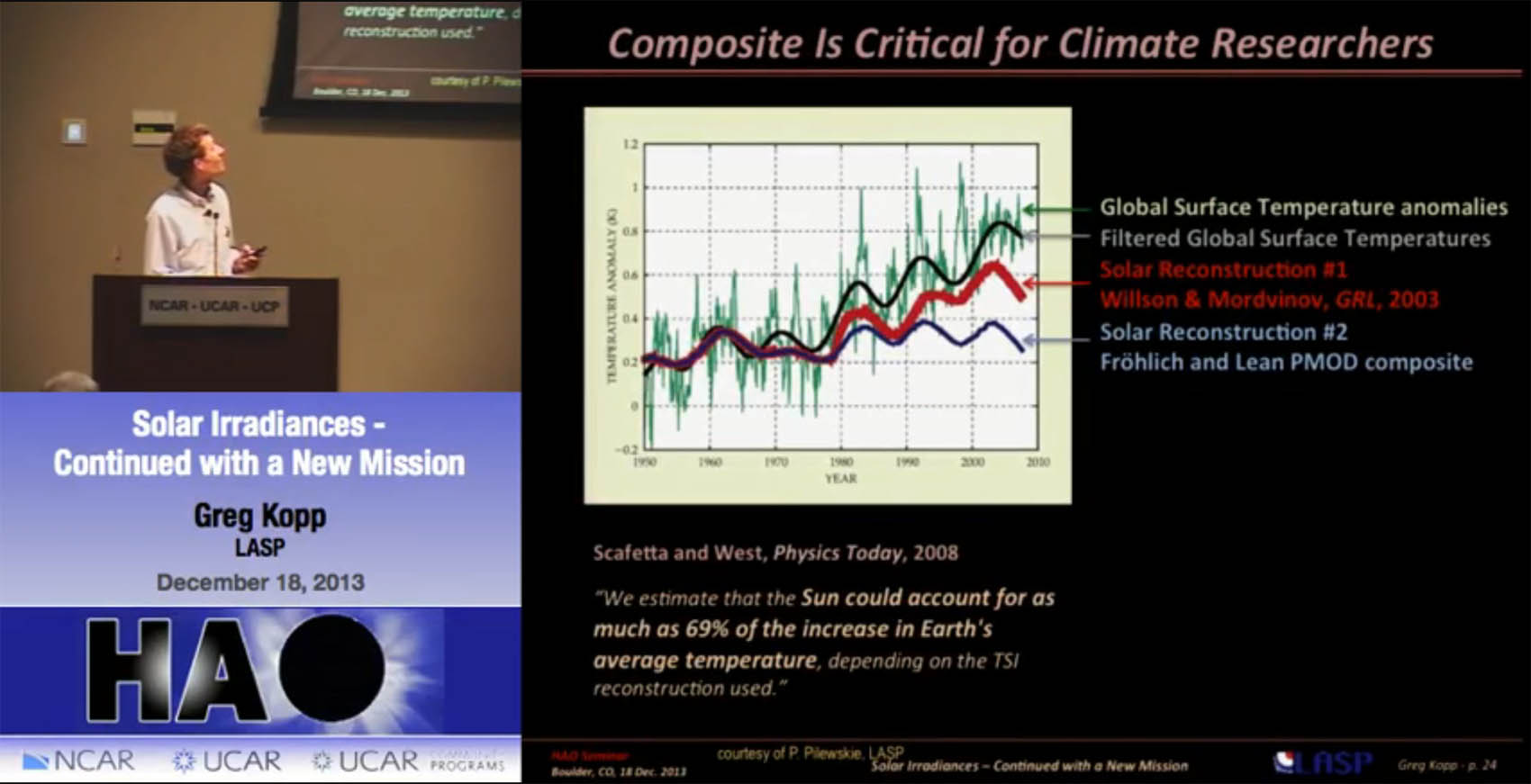
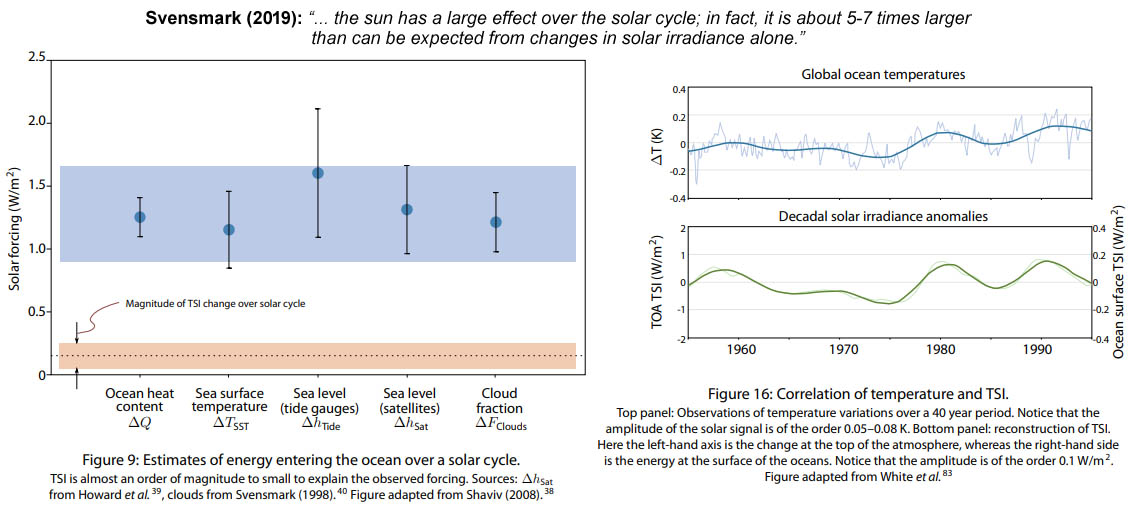
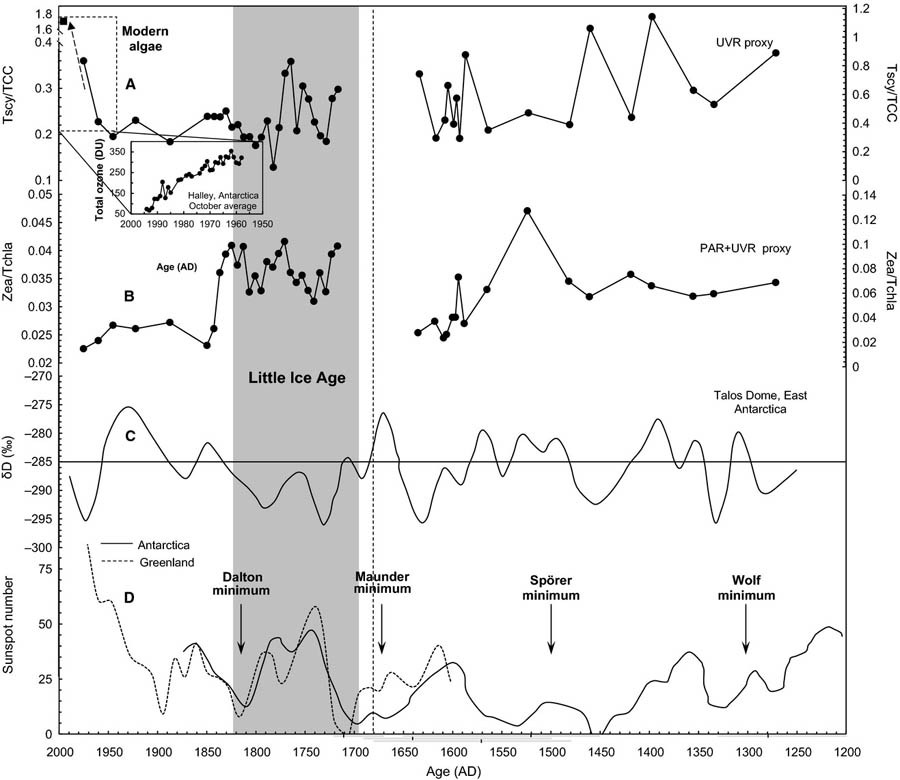






@Martijn,
Sorry ik heb de dicusie tussen jullie vandaag niet zo goed gevolgd. ik had hoger terug moeten scrollen zie ik.
Ik weet ook niet goed waarom van Gelder geen gewone complete links plaatst.
Soms is dit wat omslachtig op telefoon of tablet.
Maar ik zal in het vervolg even wat hoger terug scrollen voor ik een opmerking geef, dit was uiteraard niet de bedoeling dat ik dubbel post, en dubbele grafieken plaats.
Geen punt hoor Theo
Ik kan het alleen maar waarderen dat ook jij het artikel (met van Dorland die mijn artikel namens het KNMI heeft gereviewd) hier vanavond bent komen delen.
Dus dank voor het gebaar!
@Martijn,
Toch een interessante materie waar jij mee bezig bent, na het een en ander te lezen zijn er toch mensen die vast overtuigd zijn dat er toch een mini ijstijd komt ondanks stijging van temperatuur, al dan niet door co2.
Als je kijkt dat het na de grote ijstijd het klimaat slechts weinig schommelde kom je op een gegeven moment uit op het middeleeuws klimaat optimum, met temperaturen vergelijkbaar met nu, of zelfs hoger, te denken dat hier druiven en perziken in België, in Groenland werd akkerbouw bedreven en gletsjers waren er weinig.
Dit alles hebben ze na kunnen gaan in geschrifte tekeningen boomringen enz.
Daarna kwam de kleine ijstijd, ook hier hebben ze weer veel echte informatie terug gevonden uit het verloop er van, in geschrifte schilderijen dagboeken en noem maar op, ook op het zuidelijke halfrond hebben ze het gemerkt met een iets koudere periode.
Volgens mijn speurwerk op het net zijn toch verschillende wetenschappers er zeker van dat we eigenlijk maar net uit de kleine ijstijd zijn, en dat de temperatuur al aan het klimmen was voor het industriële tijdperk.
De vele gletsjers die nu aan het smelten zijn, daar zijn er veel van gevormd in de kleine ijstijd.
Zo heb ik nog een stukje leesvoer gevonden wat in jou richting past.
Met simpele verduidelijking.
Naast bovengenoemde Dansgaard-Oeschger en Bond cycli, heeft men nog andere cyclische variaties ontdekt. Ze hangen met zeer grote waarschijnlijkheid samen met activiteiten op de zon. Zo bestaat er een cyclus van 22 jaar, één die tussen de 80 en 90 jaar aanhoudt en nog enkele korte cycli van 4,7 – 6,4 en 8,8 jaar. Al deze cycli zijn ontdekt door variaties in isotoopverhoudingen, afkomstig van kosmische straling.
http://kijkeensomlaag.nl/index.php/ijstijden-en-ijstijdafzettingen/kleine-ijstijd
Inderdaad Theo, menig element in de uitkomst van mijn analyse is ook in de uitkomst van andere onderzoeken terug te vinden.
In mijn beschrijvingen hierboven m.b.t. de diverse meerjarige periodes heb ik de aandacht inmiddels meer specifiek gericht op de periodes rond de minima van de jaren 1890-1985; via deze periode kan ik de kern van mijn vondst m.b.t. de impact van de zon nu relatief eenvoudig gaan beschrijven.
Dit betekent dat ik hiermee o.a. de impact van de ozonproblematiek geheel naar de achtergrond kan verschuiven om tot vrijwel dezelfde uitkomst te komen.
Bij de zonneminima jaren zelf blijkt nog iets bijzonders aan de hand… wat nog minder ruimte biedt voor twijfel over de relevantie.
(Ik kan mijn argument nu ook aanscherpen op de wijze zoals ik al heb gedaan in mijn reactie zojuist n.a.v. de input van Danny; ik heb inmiddels ook een insteek gevonden waarmee het arbitraire karakter van de correctie verdwijnt – maar daar ga ik nu nog even niet verder op vooruit lopen)
En nu even wat stappen in de natuur zo lang er nog bomen staan! :-)
Reactie op je reactie van 19 mei 2020 om 23:56.
“De bandbreedte voor de schatting van de klimaatgevoeligheid voor CO2 is echter groter; eigenlijk ligt deze in de orde van 0-10 K.” Dat wordt niet ondersteund door de literatuur.
“Hiermee belanden we eigenlijk automatisch bij het punt dat er een versterkingsfactor actief is.
Voor de versterkingsfactor spreek ik over een versterkende waarde van “37,5 tot 84”.”
Precies, en zolang je die niet aannemelijk gemaakt heb, is het fysisch onmogelijk. Je hebt ideeën genoeg, maar geen enkele daarvan geeft een mechanisme waar door de aarde minder LW straling uitzendt. Want TSI zelf is te zwak.
“Kortom, ik veronderstel dat je bij je beschrijving “is fysisch onmogelijk” geen rekening hebt gehouden met de impact van de versterkende factor.” In mijn ogen verkoop je de huid al voordat je de beer geschoten hebt.
Ik hou er ook mee op. Ik vond het onzin en ik blijf het onzin vinden.
Re: Voorbijganger “Reactie op je reactie van 19 mei 2020 om 23:56.
“De bandbreedte voor de schatting van de klimaatgevoeligheid voor CO2 is echter groter; eigenlijk ligt deze in de orde van 0-10 K.” Dat wordt niet ondersteund door de literatuur.”
Toch wel hoor, want in deze lijst met 142 studies staan 8 bronnen vermeldt waarbij de bovenkant van de bandbreedte voor de klimaatgevoeligheid op 10 graad C (of hoger) wordt ingeschat en 1 bron waarbij de onderzijde van de klimaatgevoeligheid op 0 graad C wordt ingeschat:
https://docs.google.com/spreadsheets/d/1Bw2XU3FCw9a__Z5Y9YGfCWU-ohzuhFJ8_gcGyIsTECE/edit#gid=0
Re: ““Hiermee belanden we eigenlijk automatisch bij het punt dat er een versterkingsfactor actief is.
Voor de versterkingsfactor spreek ik over een versterkende waarde van “37,5 tot 84”.”
Precies, en zolang je die niet aannemelijk gemaakt heb, is het fysisch onmogelijk. Je hebt ideeën genoeg, maar geen enkele daarvan geeft een mechanisme waar door de aarde minder LW straling uitzendt. Want TSI zelf is te zwak.”
Ik heb inmiddels een andere wijze gevonden waarmee op basis van het perspectief van de zonnecyclus de versterkingsfactor kan worden ingeschat; hiervoor geldt een bandbreedte van 6 (op basis van studies waarbij de temperatuur impact van de 11-jarige zonnecyclus op 0,26 K wordt ingeschat) tot 80 (op basis van studies waarbij de temperatuur impact van de 11-jarige zonnecyclus op slechts 0,02 K wordt ingeschat).
Uitgaande van de beschrijving van Shaviv & Svensmark dat op de 11-jarige zonnecyclus een versterkingsfactor van 5-7 (gemiddeld dus 6) van toepassing is, kan de berekening wordt gemaakt dat mijn beschrijving van 1,2 K per W/m2 voor het TSI aan de top van de atmosfeer een λ impliceert voor het aardoppervlak van 6,8 K per W/m2. Wanneer hier vervolgens rekening wordt gehouden met een versterkingsfactor van 6 dan belanden dat mogen deze laatste 2 getallen door 6 worden gedeeld en vinden we voor het perspectief van het aardoppervlak een waarde van 1,14 K per W/m2… wat net binnen de bandbreedte ligt die van Dorland heeft beschreven op basis van AR5 (“λ=0.4-1.2 C/Wm-2”).
Kortom… ik hoop dat je mijn beschrijvingen kunt zijn als een soort van ‘werk in uitvoering’.
Overigens, in mijn posts hierboven van 21 mei 2020 om 18:59 en 21 mei 2020 om 23:39 heb ik nog enkele andere facetten besproken die een beetje meer zicht geven op de betrokken mechanismen.
Inmiddels ook een stevige onderbouwing gevonden in de literatuur die mijns inziens naadloos aansluit op mij beschrijvingen:
In het volgende citaat van een publicatie uit 2011 van Prof. Shaviv wordt beschreven dat dezelfde hoeveelheid energie in het perspectief van de 11-jarige zonnecyclus een temperatuur effect oplevert dat slechts 10-20% is van het resultaat in het langetermijn perspectief; kortom, voor het langetermijn perspectief is dus sprake van een versterkende factor van 5 tot 10… dit sluit mijns inziens prachtig aan op wat ik in mijn onderzoek beschrijf, want ik heb beschreven dat er voor het lange termijn perspectief sprake is van een versterkende factor die aanzienlijk groter is dan de impact van de temperatuurverschillen bij de 11-jarige zonnecyclus:
De peer-reviewed publicatie ga ik richten op de minima in de periode 1890-1985.
Bij een vergelijking tussen het 3-jarige en het 11-jarige gemiddelde rond de minima zien we vooral voor de periode 1890-1943 een opmerkelijk beeld ontstaan wanneer de correctie gericht op de secundaire minima wordt verdubbeld naar 0,246 W/m2:
http://klimaatcyclus.nl/klimaat/pics/bassie.jpg
PS. De correlatie voor deze periode bedraagt bij de 3-jarige waarden 0,963 en bij de 11-jarige waarden 0,922; kortom, wanneer rekening wordt gehouden met een toename van de omvang van de correctie (i.v.m. hogere TSI waarden bij de gemiddelde waarden over een langere periode) dan wordt duidelijk de periode 1890-1933 duidelijk lagere waarden toont bij zowel de temperatuur als de TSI.
97,4% van de opwarming tussen de 1912 en 1985 minimum jaren wordt verklaart door de zon:
http://klimaatcyclus.nl/klimaat/pics/1890-1985-minimum-years-for-HadSST3-vs-LISIRD-TSI-with-corrected-secondary-minima-values.jpg
Deze illustratie beschrijft tevens dat de na de gebruikte correctie de verklaarde variantie dezelfde waarde heeft als bij de primaire en secundaire minima afzonderlijk, namelijk: 91%.
Martijn (21 mei 2020 om 11:45),
“Nee” is je antwoord en dat is uiteraard het enige juiste antwoord. Het betekent dat de pieken en dalen in het temperatuur patroon dat je zag in De Bilt klimaatruis is en niet ten gevolge van de zon. Je ziet die pieken en dalen immers niet terug in dezelfde jaren in het mondiale plaatje
Foei Ronald,
Je hebt kennelijk niks geleerd van de heldere uitleg die Martijn hiervoor al gegeven heeft.
Lees de analyse van Martijn nog maar eens terug.
Helder, Willem?
Ik zie woorden als: “waarschijnlijk”, “ik vermoed”, “het zou mij niet verbazen”, “ik ga er hierbij nu even vanuit”, “speculatief”, “kan ik enkel speculeren”, “mogelijk”. Ik kan dat niet verhelderend noemen, maar meer als: ik heb eigenlijk geen idee.
Als AMO en PDO volgens Martijn een substantiële bijdrage leveren aan het temperatuurpatroon, dan spelen deze ook een rol rond de lokale zonneminima en dan lijkt het me noodzakelijk deze mee te nemen in zijn analyse. Maar, ik ben ze niet tegengekomen in zijn artikeltje …….. ?
Ronald, aanvankelijk sprak je over een “gedachtenexperimentje”… maar het lijkt inmiddels niet veel meer dan een tunnelvisie redenering waarbij je met je eigen woordkeuze nauwelijks ruimte gaf om een ander antwoord dan ‘nee’ te geven.
Uit dit soort van woordspelletjes wek je in mijn ogen de indruk dat de materie je inhoud nauwelijks interesseert.
Nogmaals, volgens de definitie vallen patronen buiten het fenomeen ‘klimaatruis’… zelfs wanneer de fysische oorzaak van het patroon onbekend zou zijn, maar in dit geval is hiervan eigenlijk geen sprake want de regelmaat van het bodempatroon volgt in feite “exact” de 22-jarige magnetische cyclus.
Ik heb er al op gewezen dat het patroon ook van toepassing is op Centraal Engeland; ik kan er inmiddels aan toevoegen dat het verloop van het faseverschil t.o.v. de secundaire zonneminimum jaren vrijwel exact hetzelfde is in de Bilt en Centraal Engeland: bij 1902 valt de temperatuurdip samen met het minimum; vervolgens 3x enkele jaren vlak voor het secundaire zonneminimum van 1923, 1943 en 1965; bij 1985 valt de temperatuur dip samen met het zonneminimum en tenslotte bodemt de temperatuur bij het 2008 secundaire minimum 2 jaar later in 2010.
Kortom, bij de Bilt en Centraal Engeland wordt vrijwel exact hetzelfde patroon aangetroffen en dit heeft dus helemaal niets van doen met ‘klimaatruis’.
Martijn,
het gedachte-experiment heeft jouw tunnelvisie blootgelegd. Je hebt in de discussie patronen geïntroduceerd (AMO en PDO) die invloed hebben op de mondiaal gemiddelde temperatuur tijdens zonneminima. De invloed van deze patronen heb je echter niet meegenomen in de analyse (correlaties) van het laatste artikeltje en dus is het zeer wel mogelijk dat je de correlatie tussen de mondiaal gemiddelde temperatuuranomalie en zonneminima hebt overschat dan wel onderschat. Zeer vermoedelijk overschat zoals blijkt uit de verdere analyse hieronder.
Dat Centraal Engeland eenzelfde temperatuur patroon kent als De Bilt is logisch, Nederland en Engeland zijn onder invloed van dezelfde weer regimes. Het Belgische Ukkel laat om dezelfde reden ook eenzelfde patroon zien. En zoals je weet is weer in de context van klimaat ….. ruis. Dat plaatsen elders in de wereld een ander patroon laten zien toont dat wel aan. Dus helaas Martijn, je ziet patronen die je wilt zien in ….. klimaatruis.
1965 (secundair zonneminimum) was in De Bilt verre van een lokaal minimum (1963 was veel kouder) en mondiaal gezien ook niets bijzonders t.o.v. omliggende jaren. Dat laten jouw plaatjes óók zien.
De eigenschappen van de zon zijn overal hetzelfde, of die nu schijnt in De Bilt, Kimch’aek of Johannesburg. De impact van de zonneminima op de temperatuuranomalie blijkt dus bescheiden wanneer temperatuurreeksen op verschillende locaties met elkaar vergeleken worden. En dat is niet verrassend omdat andere fenomenen, die je hebt veronachtzaamt in je laatste artikeltje, ook zeker een rol spelen.
Het gedachte-experiment is dus zeer leerzaam gebleken en heeft een aantal zwaktes in jouw analyse blootgelegd.
Ronald, voor mij is duidelijk dat je retoriek gebruikt waarbij je zowel op het niveau van de data als het niveau van de definities de feiten negeert.
De AMO en PDO bracht ik enkel ter sprake i.v.m. het faseverschil dat zichtbaar is bij de lokale data t.o..v. de zonneminima jaren maar eigenlijk dient dit nog verder te worden genuanceerd want de TSI minima en maxima vallen lang niet altijd samen met de minima van de zonnevlekkencyclus en dit geldt ook voor het poloïdale magnetische veld. Verder hebben we voor dit onderzoek überhaupt nog niet naar de data sets van andere locaties in de wereld gekeken.
MIjns inziens houd je jezelf nogal opzichtig voor de gek want je zogenaamde “gedachtenexperimentje” blijkt in feite helemaal niets om het lijf te hebben: je hebt immers enkel een vraag gesteld waarbij de formulering slechts tot 1 antwoord kon leiden… en daar had je mijn input echt niet voor nodig.
Helaas voor jou Martijn, heeft het gedachten experiment de zwaktes in jouw analyse blootgelegd. Door niet concreet in te gaan op mijn punten geef je dat impliciet ook toe. Het kan natuurlijk ook zo zijn dat je mijn punt niet hebt begrepen.
Wellicht helpt het door je een korte vraag voor te leggen (waarop wederom twee antwoorden mogelijk zijn).
Denk je dat AMO en PDO invloed hebben op de mondiaal gemiddelde temperatuur tijdens zonneminima?
Ronald, je stelt hier enkel een vervolgvraag op een aspect in het antwoord dat ik eerder gaf.
Je vraag is mijns inziens zowel pretentieus als irrelevant.
(Je houd jezelf hier denk ik opnieuw voor de gek want de formulering laat deze keer nauwelijks ruimte om een ander antwoord te geven dan ‘ja’, maar tegelijkertijd zegt waarschijnlijk helemaal niets over de relevantie van het antwoord)
Martijn, als je de vraag met “ja” beantwoordt dan is dat wel degelijk zeer relevant. Stel je nu eens voor dat de correlatie van AMO/PDO met de mondiaal gemiddelde temperatuur tijdens zonneminima niet verwaarloosbaar is, wellicht zelfs substantieel, wellicht zelfs hoog, wat verklaart dan het temperatuurverloop tijdens de zonneminima? De zon of AMO/PDO? of een combinatie van beide? In het laatste geval, in welke verhouding?
Die vragen heb je niet bestudeerd, laat staan beantwoord en dus is de titel van jouw artikeltje wel héél voorbarig.
Ronald, bij het stellen van je vraag lijk je je niet bewust van het feite dat de AMO en PDO uit fase lopen met de temperatuur, wat verklaart waarom beide geen prominente rol spelen in klimaatmodellen.
(In feite probeer je hier met een nogal oppervlakkige redenering de indruk te wekken dat de AMO en PDO samen of afzonderlijk een sterker verband met de temperatuur zouden kunnen hebben dan de zon; je doet jezelf opnieuw tekort want dit is slechts een vorm van fantasie – waarbij een wensgedachte een rol kan spelen – want feitelijk gaat dit getalsmatig helemaal nergens over. Maar inmiddels is dit voorbeeld in mijn ogen wel typerend voorbeeld hoe je vrijwel voortdurend vrijblijvend alle kanten opvliegt met je eigen gedachten… meestal op zoek naar verklaringen waarmee je op je eigen wijze weg denkt te kunnen lopen van de getalsmatige feiten. Zo kun je grenzeloos via nietszeggende retoriek voortdurend altijd alles ontkennen op basis van argumenten die eigenlijk op geen enkele wijze hout snijden. Maar uiteindelijk doe je met zo’n vrijblijvende benaderingswijze waarschijnlijk vooral jezelf daarmee te kort want dit heeft allemaal weinig tot niets van doen met de realiteit)
Wel Martijn, ik heb getracht in deze discussie jouw wensdenken onder ogen te brengen. Het komt niet binnen. Het begon met klimaatruis, waarin jij signaal meende te zien. Daarna over bestaande patronen die je simpelweg hebt genegeerd. Je hebt de invloed van AMO/PDO op de mondiaal gemiddelde temperatuur ten tijde van zonneminima niet onderzocht en voor het gemak maar aangenomen dat deze geen rol spelen. Deze vorm van wensdenken is wetenschappelijk onverantwoord en daarmee is de titel van jouw artikeltje héél voorbarig.
Zie wat dat betreft ook Ferdinand Engelbeen, eerder vandaag:
“Op basis van bovengenoemd boek was ik ook lange tijd voorstander van de dominante rol van de zon op ons klimaat, maar als de zonneactiviteit afneemt, terwijl de temperatuur blijft stijgen, is dat niet vol te houden…”
https://www.climategate.nl/2020/05/de-mondiale-co2-huishouding-mooie-getallen-geveinsde-zekerheid-maar-hoogst-twijfelachtig-deel-2/comment-page-1/#comment-2314224
Alles wijst erop dat je de rol van de zon zwaar overschat.
Ferdinand houdt zich naar eigen zeggen al zo’n 40 jaar bezig met klimaat. Jij komt net kijken. Gepaste bescheidenheid lijkt me dus op z’n plaats. Ik heb je dat proberen bij te brengen, maar het is niet gelukt. Jammer dan …..
Ronald, je gebruikt hier opnieuw een retorisch argument door te claimen dat de zonneactiviteit zou zijn afgenomen.
Feit is in ieder geval dat dit geenszins van toepassing is op de TSI minima van de zonnestraling (lees: het basisniveau van de zonnestraling).
Kortom, je gebruikt een argument waarbij je geen rekening houdt met zowel de ACRIM-PMOD controverse als de uitkomst van mIjn onderzoek.
PS. De redenering van Engelbeen is dus onjuist bezien vanuit het perspectief van de minima volgens de LISIRD TSI.
Ferdinand Engelbeen gaat uit van de totale bijdrage van de zon en niet een ge-cherry-picked deel dat leidt tot een vooraf vastgestelde gewenste uitkomst door vele onderdelen van het klimaatsysteem te negeren. Dat leidt tot een fundamenteel verschil van inzicht, en daar laat ik het verder bij.
Ik heb inmiddels nog een leuke illustratie gemaakt die de impact van een correctie specifiek gericht op de minimum jaren zowel visueel als getalsmatig duidelijk maakt t.o.v. de situatie zonder de correctie:
http://klimaatcyclus.nl/klimaat/pics/1890-1985-minimum-years-for-HadSST3-vs-LISIRD-TSI-with-and-without-corrected-secondary-minima-values.jpg
@Martijn
@Ronald,
Dat van Ferdinand, en nog een aanvulling van Guido, heb ik ook gelezen.
Maar Martijn heeft het toch over de 22 jarige cyclus, en zij hebben het over de normale 11 jarige cyclus.
Ik meen toch dat ik het zo begrepen heb.
Maar Chris word ook trouwens compleet onderuit gehaald.
Het blijft een moeilijke materie.
Maar heb ik het goed Martijn dat jij het over de 22 jarige cyclus hebt?
Inderdaad Theo, uit mijn analyse blijkt dat de 22-jarige cyclus cruciaal is (+ dat de 11-jarige cyclus grotendeels verantwoordelijk kan worden gehouden voor het ontstaan van ‘klimaatruis’, waarschijnlijk via de invloed van zonnewind).
PS. Engelbeen is welkom op mijn onderzoek te reageren maar ik ga zelf voorlopig enkel contact zoeken met deskundigen op het terrein van de zon omdat zij de impact van de wisselingen van de magnetische polen van de zon waarschijnlijk veel beter kunnen beoordelen. Het moge inmiddels duidelijk zijn dat over dit onderwerp in de rapporten van het IPCC niet wordt gesproken want zelfs de 22-jarige cyclus wordt überhaupt niet eens genoemd.
Martijn, ik zie ieder keer de bevindingen van de 11 jarige cyclus als ik eens op het net een beetje aan het rondsnuffelen ben, ja en dan krijg je weer de tekst dat het geen zoden aan de dijk zet.
Maar van die 22 jarige cyclus daar vind je bitter weinig van, ja het enige zinnige waar ik laatst hier de link van gepost had, die man had vergelijkbare conclusie met jou.
Maar goed ik volg het verder. :-)
Hij zal zijn website niet goed hebben bijgehouden. Inmiddels is Engelbeen tot een ander inzicht gekomen (met dank aan Ronald)
“Op basis van bovengenoemd boek was ik ook lange tijd voorstander van de dominante rol van de zon op ons klimaat, maar als de zonneactiviteit afneemt, terwijl de temperatuur blijft stijgen, is dat niet vol te houden…”
Ronald, ik vrees dat je ook m.b.t. de kijk van Ferdinand Engelbeen enigszins voorbarig bent geweest met de interpretatie van zijn woorden want op zijn website staat het volgende vermeld:
En:
PS. Nu ik dit heb gezien zou het mij niet verbazen wanneer Engelbeen niet op de hoogte is van de ACRIM-PMOD controverse, want ik vermoed dat op de laatste pagina is gewerkt met een data set voor de zon waarbij de minima in de laatste decennia een neerwaarts verloop tonen… welke niet representatief is voor wat de satellietmetingen sinds 1979 hebben laten zien.
Je interpreteert er weer lekker op los Martijn, maar je tekstjes van Engelbeen bevestigen mijn conclusie: “Dat leidt tot een fundamenteel verschil van inzicht”
Kwestie van: ik zie, ik zie wat jij niet ziet?
http://boels069.nl/Q%20and%20Tk%20vs%20Solar%20Elevation%20KNMI-Cabauw%202004-2020.pdf
De X-as is de zonnestand (vrijwel een constante, ruim binnen 0,1 graad).
Rechter Y-as: oppervlaktetemperatuur
Oranje stippen: oppervlaktetemperatuur tot -17,9 graden zonnestand
Gele stippen: oppervlaktetemperatuur bij zonnestand van -18 tot +18 graden (astronomische schemering)
Groene stippen: oppervlaktetemperatuur bij zonnestand vanaf 18,1 graden
Linker Y-as: insolatie
Grijze stippen: insolatie bij zonnestand van -18 tot +18 graden (astronomische schemering)
Blauwe stippen: insolatie bij zonnestand vanaf 18,1 graden
Interessant grafiekje Boels, maar ik mis een beschrijving m.b.t. wat jij zelf uit deze grafiek denkt af te kunnen lezen.
Ik vraag mezelf in eerste instantie vooral af of we aan deze grafiek ook iets kunnen aflezen dat betrekking heeft op het verloop van de tijd voor de periode 2004-2020, wellicht?
@Martijn van Mensvoort:
Ik ga proberen er een verhaaltje bij te schrijven, maar ik laat het even bezinken …
Vanaf het moment dat het (voor mij) duidelijk werd dat de zonnestand de enig goede berekenbare variabele is in de complexiteit van het aardse klimaat (naast de breedte- en lengtegraad van een meetpunt).
Mijn veel eerdere kritiek op het gebruik van kalenderjaren (en kalendermaanden) die immers berekende waarden op x-decimalen achter de komma nogal futiel maken en leidde tot de voor de handliggende “vondst”, nl. gebruik een periode van 4 tropische jaren.
Om de 1461 dagen is de zonnehoek (“elevation”) dezelfde; m.a.w. de invloed van de zonnestand op de oppervlakte temperatuur is constant (uiteraard zonder nog rekening te houden met de “irradiation”, hoewel die verdisconteerd zou moeten zijn in de gemeten “insolation”.
Ik heb inmiddels ook gekeken naar de etmaalgemiddelde oppervlaktetemperatuur vanaf 1960 (De Bilt).
Daar wordt voor het maximum en het minimum van de dagtemperaturen óók de betreffende uurwaarde opgegeven; daarmee kan ik de zonnestand herleiden voor TN en TX.
Ter aanvulling: ik gebruik voor de “elevation” een oud Excelprogramma met VBA van NOAA; bruikbaar vanaf 1900.
De Bilt geeft pas “insolation”-waarden vanaf juli 1967; dat is de reden dat ik vanaf 1960 de gegevens gebruik.
Ik heb dan 15 perioden van 4 kalenderjaren tot mijn beschikking.
Ik heb voor Cabauw gekozen omdat er boordevol gegevens zijn voor toekomstig gepuzzel:
http://projects.knmi.nl/cabauw/bsrn/quicklooks/BSRN_dy.php?csrc=bsrn&day=2020-05-12
Van Cabauw gebruik ik data vanaf 2004.
Zie jij sprongen rondom de schrikkeljaren, Boels? Zo niet, dan kun je jouw tijd beter besteden dan zoeken naar de y>x decimaal.
@Ronald:
Laat mij toch de eigen tijd verspillen ;-)
Kernpunt is wel: hanteert de klimatologie wel de juiste kalendercijfertjes; wordt het geen tijd om ook bij de aardse waarnemingen de satelliettijd te hanteren?
In de wetenschap heb je niets aan kalenderjaren en kalendermaanden.
Ik erger mij aan resultaten tot op 3 of 4 decimalen achter de komma (uiteraard verdrinkt de ogegeven nauwkeurigheid in de onzekerheden).
De enige berekenbare grootheid is de zonnestand, afhankelijk van de liogging van de meetlokatie en de “epoc”.
Winkelen bij astronomen lijkt mij een goed idee.
Boels,
de foutmarges zijn inderdaad matig/niet te vinden in wetenschappelijk minder relevant werk.
Toch zou ik je willen adviseren eerst maar eens een grove inschatting te maken van het te verwachten effect. Het zou toch zonde van de tijd zijn om na maanden ploeteren te ontdekken wat al op dag 1 duidelijk had kunnen zijn.
@Boels,
Ik zie dat je ook nog met je project bezig bent, ik had al gedacht dat je er waarschijnlijk mee gestopt was.
Tenminste ik denk dat dit nog bij dat project hoort met dat exel bestand wat ik toen niet gerund kreeg op de tablet.
Er word hard gewerkt achtet de coulissen! :-)
@Theo:
Ik noem het geen project, want dan zou ik ergens tot een afronding moeten komen ;-)
Het gaat mij meer om het eigen begrip/onbegrip en hoe de doorsnee klimatologie tot conclusies komt.
Zelfs met de zonnestand als uitgangspunt blijft het klimaat een extreem complex chaotisch fenomeen.
Wel kan de “global temperature” met de huidige definitie bij het afval gezet worden.
In de laatst getoonde grafiek is geen aandacht besteed aan de opwarming; een volgende stap is het stoeien met anomaliën.
Ik heb van Cabauw 4 perioden van 1461 dagen; alle meteodata van de periodes 2, 3, 4 en 5 verminder ik met die van periode 1.
Dat wordt smullen ;-)
Of niet.
Oké @Boels, duidelijk.
Trouwens dat rekenen zo ver achter de komma vind ik ook overdreven zeker als het over temperaturen van het verleden gaat toen er nog niet eens echte zuivere metingen mogelijk waren.
Ik begrijp dat ze hebben liggen te middelen, maar dan nog.
En die 1461 dagen, ik meen toch dat je die al mooi in een Exel bestand had staan, of zit ik nu helemaal fout?
Ach ja en ieder mag ook zelf zijn bevindingen hier posten vind ik, de weg die ze nu aan het inslaan zijn zal voorlopig toch niet snel meer veranderingen in komen, het enige waar je nog op kan hopen is verzachting.
Doelstellingen worden toch niet gehaald, daar hoef je geen geleerde voor te zijn.
In het begin zal het nog wel lukken, maar daarna zal het voor hun zeer moeilijk gaan worden, of het welzijn van de burger moet helemaal ten gronde gaan.
Boels, het kwartje is gevallen bij mij:
Ik begrijp nu wat je in gedachte hebt; je verondersteld dat een kalenderjaar dusdanig onregelmatig verloopt in het perspectief van de kosmos dat de zonnestand kan fungeren als een soort van ijkpunt en controlemechanisme in het perspectief van het maken van vergelijkingen tussen o.a. verschillende jaren, kalenderdagen, etc.
Formuleer ik het zo goed?
PS. Jij denkt vast ook aan de invloed van fase verschillen veronderstel ik? Ik kan zelf echter niet overzien hoe groot die faseverschillen kunnen worden in dit perspectief.
Het is dan ook geen “global temperature”, Boels, maar global mean temperature. Dat is iets heel anders en prima gedefinieerd. Bovendien neemt de nauwkeurigheid van de ‘mean’ toe met wortel-N, met N het aantal datapunten. Als N maar groot genoeg is dan kan de uitkomst met veel cijfers achter de komma nog altijd prima statistisch significant zijn.
In het perspectief dat er perspectief moet zijn om überhaupt van perspectief te kunnen spreken heb je het in correct perspectief geformuleerd, Martijn. Althans, bekeken vanuit mijn perspectief ;-)
@Ronald:
Het zijn maar woorden, maar toch het IPCC heeft het “global warming” in “Summary for Policymakers of IPCC Special Report on Global Warming of 1.5°C approved by governments”.
Bovendien neemt de nauwkeurigheid van de ‘mean’ toe met wortel-N, met N het aantal datapunten.
Dat zegt mij niets, het aantal meetplaatsen is nogal onevenredig verdeeld over de planeet.
Beetje schofferend: als men 100 miljard meetpunten met een gigantische hoeveelheid aan jaarlijkse data verkeerd simuleert dan zegt het nog niets.
De statistiek blijft geduldig.
dan heb je het over bias, Boels. Dat is wat anders.
@Martijn van Mensvoort:
… ijkpunt..
Precies!
Merkwaardig blijft dat de satelliet-klimatologie daar helemaal geen problemen mee heeft!
Waarbij in groter verband de stand van de aardas en de verschuiving van de geografische positie ook een rol speelt; bv. bij paleometingen.
De rekenmethode die ik gebruik is de volgende.
Ik haal uit de dataset van Cabauw (ter grootte van 4 maal 35064 uurwaarden):
Per periode van 1461 dagen en per uur:
– de zonnestand op 0.1 graad
– de insolatie
– de temperatuur in Kelvin
Dan gebruik ik 95% van de data op basis van de aantal keren dat een specifieke zonnestand voorkomt; daarmee verwijder ik “outliers”.
Per zonnestand bepaal ik het rekenkundig gemiddelde van:
– de insolatie
– de temperatuur
Per zonnestand constateer ik een bruikbare RSQ (>0,8) tussen zonnestand van zowel insolatie als temperatuur.
Waarmee ook de onderliggende relatie tussen insolatie en temperatuur blijkt.
Ik ga de faseverschuiving (“atmosferische traagheid”) nog nader bekijken.
Voor De Bilt is het faseverschil tussen de dagelijkse gemiddelde maxima van insolatie en temperatuur ongeveer 2,5 uur (met What-if van Excel kom ik op 2,6 uur).
Mooi Boels!
Fijn dat je intentie voor mij nu dan eindelijk duidelijk is.
De relevantie van de technische details die je gebruikt is voor mij nog helemaal niet duidelijk.
Is het wellicht mogelijk dat je uiteindelijk ook een grafiekje gaat tonen dat een beeld schetst van de ontwikkeling chronologisch in de tijd?
“Waarmee ook de onderliggende relatie tussen insolatie en temperatuur blijkt.”
temperatuur hangt niet alleen af van insolatie, maar van vele andere factoren.
@Ronald:
Is dat je nieuwe tijdverdrijf: open deuren intrappen?
Een onderliggende relatie sluit andere factoren niet uit.
Wel is de insolatie een resultante van alle “filters” die de zonne-instraling tegenkomt.
Wel jammer dat de langgolvende infraroodstraling straling niet gemeten wordt, dan kon de CO2-hype ook aangepakt worden.
Ja hoor Boels, die wordt wel gemeten. Je bent er al vele malen op gewezen, maar je wilt het blijkbaar niet weten?
Ha Boels,
Ik merk dat je gaat aantonen dat het overdag warmer is dan ’s nachts. Dat wist ik nog niet.
@Voorbijganger:
Ik merk dat je gaat aantonen dat het overdag warmer is dan ‘s nachts. Dat wist ik nog niet.
Ik had al zo’n vermoeden ;-)
Ik ben de beroerste niet, dus ..
@Ronald:
In de openbare datasets van het KNMI ben ik het niet tegengekomen.
Bij het onderzoek in Cabauw is dat wel het geval.
@Martijn van Mensvoort 26 mei 2020 om 14:28
Ik doe nu voornamelijk bewerkingen met de gegevens van Cabauw over 2004 tot 2020 (4 perioden van 1461 dagen, per perioden 35064 uurggegevens).
Heb gekeken naar de voortschrijdende trend van de laatste 3 perioden t.o.v. de eerste.
Het lijkt er op dat de meeste opwarming plaats vindt tijdens de astronomische schemering.
Te mooi om waar te zijn, dus ik zal wel iets verkeerds gedaan hebben ;-)
Interessant Boels, het zou bijzonder worden als je visueel zou kunnen laten zien dat de toegenomen opwarming vooral heeft plaatsgevonden tijdens de astronomische schemering maar het is al wel bekend dat de opwarming vooral ’s nachts en in de herfst/winter de grootste impact heeft gehad.
(Ik vraag me wel af of ik je wel goed begrijp, want logischerwijs zou zo’n conclusie eigenlijk moeten impliceren dat je de 24 uurs data categorisch in kaart hebt gebracht, terwijl je enkel spreekt over data rond de astronomische schemering…???)
@Martijn van Mensvoort:
Ik gebruik alle uurgegevens, 24 stuks per dag.
Die verdeel ik op basis van de zonnestand in 3 delen (18 graden; oftwel “nacht”, “schemer” en “dag”) en bepaal het rekenkundige gemiddelde per zonnestand.
Ik zal over een paar dagen een update van de grafiek(en) geven, ook al door een “administratieve” fout van mij: de gebruikte zonnestand werd bepaald voor tijdzone UTC-0 en dat moet bij nader inzien UTC+1 zijn.
@Boels, vergeet ook de zomertijd niet GMT plus 2. :-)
@Theo:
Dank!
Gelukkig worden alle meteodata in UTC/GMT+0 opgegeven.
Daarom was het best wel dom van mij om de zonnestanden ook uit te rekenen in UTC/GMT+0.
Omdat het nogal wiedes is dat de geografisch positie van een meetveld onveranderlijk is ;-)
@Boels,
Ik weet niet of dat dom is, trouwens dom bestaat niet echt.
Bijna alles wat over de wereld gaat, zelfs communicatie viegtuigen satellieten logboeken, noem maar op werkt met GMT tijd, zolang het er maar bij vermeld staat.
Of je moet natuurlijk echt met locale tijd willen werken.
Ik neem aan dat jij dat in dit geval zo wilt.
Onze tijdzone voor terug te rekenen is in principe wel makkelijk, en dicht bij onze lokale tijd.
@Theo:
Inderdaad, logboeken zijn in UTC (=GMT onder andere vlag).
Daardoor zijn bv. meteo/klimaatgegevens onderling goed vergelijkbaar en kan een mondiaal plaatje ontstaan.
Of je wel of niet de lokale tijd gebruikt maakt niet zoveel uit als je de tijdzone maar vermeldt.
Dan moet je natuurlijk de zonnestand wel koppelen aan de geografische positie van het meetstation, ongeacht de tijdzone.
@Boels,
Ja daar heb je helemaal gelijk in, zolang je in de tijdzone blijft kan je inderdaad lokale tijd aan houden, het enige vervelende daar aan is dat je met de zomer en wintertijd zit.
Als je werk net in deze overgang ligt met b.v een grafiek is dit niet erg praktisch.
Maar ik begrijp nu wat je bedoeld.
Het secundaire zonneminimum jaar 1879 was zowel in de Bilt als in Centraal Engeland het koudste jaar van de afgelopen 150 jaar, zie:
http://klimaatcyclus.nl/klimaat/pics/de-Bilt-%5BKNMI%5D-and-Central-England-%5BHadCET%5D-show-temperature-lows-near-secondary-solar-minimum-years.jpg
PS. Voor de Bilt geldt dat sinds het ontstaan van het gat in de ozonlaag in 1979 het secundaire zonneminimum jaar 1985 het koudst is geweest en daarna volgt het primaire zonneminimum jaar 1996. Bij Centraal Engeland behoren 1985 en 1996 beide tot de 5 koudste jaren vanaf 1980.
(De zonne-nihilisten mogen als ontkennen naar eigen inzicht, maar de feiten zijn helder)
Het temperatuur effect van de zonnecyclus blijkt op basis van de gemiddelde waarden in de Bilt en Centraal Engeland bij de secundaire minima een “perfect” regelmatige curve op te leveren wanneer wordt gewerkt met het gemiddelde van het jaar direct voor en direct na het minimum + hetzelfde principe voor de overige jaren
Het temperatuurverschil tussen het secundaire minimum jaar en 5 jaar voor en na het minimum bedraagt maar liefst 0,74 graad Celsius.
Bij de primaire minima wordt een soortgelijk effect aangetroffen echter het temperatuur verschil is daar ongeveer 0,53 graad C echter dit maximale verschil manifesteert zich daar pas na 6 jaar; bovendien is het verloop bij de andere jaren ook veel grilliger.
Ik heb geen idee hoe ze bij het KNMI denken over het temperatuurverschil rond de minima, maar nu ik zicht heb gekregen op de aarde van de grillige verschillen tussen de secundaire en primaire minima zou het mij niet verbazen als ze op basis van 11-jarige cyclus ook hier uit gaan van een veel kleiner temperatuureffect (wellicht in de orde van 0,1 graad Celsius voor de BIlt).
PS. De 22-jarige cyclus blijkt dus ook hier weer de sleutel om het lokale temperatuureffect van de zonnecylcus goed in kaart te brengen… en te kunnen begrijpen.
Je kunt Ukkel er ook in plotten. Ik voorspel je, dat ziet er hetzelfde uit.
Ook in Groenland zien we scherpe bodem patronen bij respectievelijk: 1949/1950, 1972, 1993 en 2015 (op basis van de data van zowel de hoofdstad Nuuk als het nabij gelegen Egedesminde).
Kortom, respectievelijk bij de primaire minima: 4 jaar voor P-minimum 1954, 4 jaar voor P-minimum 1976, 3 jaar voor P-minimum 1996 en 2 jaar voor S-minimum 2017.
Het patroon manifesteert zich dus ook bij Groenland met zeer regelmatige pauzes van respectievelijk: 23/22 jaar, 21 jaar en 22 jaar.
Overigens, ook hier weer een fase verschil echter nu rondom de primaire minima.
http://klimaatcyclus.nl/klimaat/pics/groenland-temperatuur-ijsland-spitsbergen.jpg
PS. Dus van een hemisferen effect is geen sprake, de fase verschillen lijken gekoppeld aan verschillende delen van de oceaan basins; van belang is vooral dat het patroon zich lokaal vooral manifesteert bij één van beide minima en dus niet bij beide. Een inschatting op basis van de 11-jarige cyclus leidt hierbij automatisch tot een onderschatting van het effect… dus hieruit blijkt dat het in feite een fundamentele flater berust om inschattingen te willen maken voor de invloed van de zon enkel op basis van de 11-jarige cyclus.
Enkel via de 22-jarige cyclus kan de invloed van de zon grondig worden bestudeerd… terwijl de meeste onderzoekers hiervoor geen enkel oog lijken te hebben; om verder maar te zwijgen over hoe de invloed van de zon in klimaatmodellen is verwerkt, waarin wel oog is voor de lokale situatie doch enkel op basis van de 11-jarige cyclus.
Volgens mij maakt dit duidelijk waarom men stelt dat de invloed van de 11-jarige zonnecyclus “onvoldoende” wordt begrijpen.
(Zolang met de 22-jarige zonnecyclus bij het IPCC buiten beeld houdt… blijft de situatie ongewijzigd)
Dan wordt het nu tijd voor een ander werelddeel, laten we zeggen oost-Azië. Tokyo bijvoorbeeld.
Onder het motto ‘U vraagt, wij bezorgen’:
De Tokyo bodems:
1984 (= 5 jaar na secundaire minimum jaar 1979)
1906 (= 4 jaar na secundaire minimum jaar 1902)
1925 (= 2 jaar na secundaire minimum jaar 1923)
1945 (= 2 jaar na secundaire minimum jaar 1943)
1965 (= het secundaire minimum jaar 1965)
1984 (= 1 jaar voor secundaire minimum jaar 1985)
2003 (= 5 jaar voor secundaire minimum jaar 2008)
https://data.giss.nasa.gov/cgi-bin/gistemp/stdata_show_v4.cgi?id=JA000047662&dt=1&ds=14
Dus ook hier weer een soortgelijke regelmaat welke gepaard gaat met een consequente verschuiving van het fase verschil, waarbij in dit geval logischerwijs de PDO een rol zou behoren te spelen (terwijl bij de Bilt, Centraal Engeland en Groenland logischerwijs de AMO en of NAO een rol zou behoren te spelen).
Als je eenmaal begrijpt hoe die 22-jarige cyclus zich lokaal manifesteert (met een consequente verschuiving van het faseverschil) dan wordt het plots relatief eenvoudig om de patronen tamelijke exact te beschrijven.
PS. Dus Ronald-Ruis, ik neem aan dat het nu tijd wordt voor een bezoekje op het zuidelijk halfrond, laten we afspreken bij … (pijltje gegooid & het valt op de kaart bij)… Buenos Aires!??? (LOL)
Ho… voordat we doorvliegen naar Buenos Aires… vergat ik bijna te benoemen dat het faseverschil bij Tokyo de andere kant op beweegt t.o.v. de Bilt, Centraal Engeland & Groenland (waardoor de tussenliggende periodes bij Tokyo net een jaartje te kort lijken te zijn).
De Buenos Aires temperatuur bodem jaren:
M.b.t. de secundaire minima:
1898 (= 4 jaar voor secundair minimum jaar 1902)
1924 (= 1 jaar na secundaire minimum jaar 1923)
1938???
1964 (= 1 jaar voor secundaire minimum jaar 1965)
1984 (= 1 jaar voor secundaire minimum jaar 1985)
M.b.t. de primaire minima:
=> 1912 (= primair minimum jaar 1912)
=> 1931 (= 2 jaar voor primair minimum jaar 1933)
=> 1955 (= 1 jaar na primair minimum jaar 1954)
https://data.giss.nasa.gov/cgi-bin/gistemp/stdata_show_v4.cgi?id=AR000875850&dt=1&ds=14
Er gebeurd bij Buenos Aires duidelijk vanalles rond de minima jaren; helaas ontbreekt de data voor het meest recente secundaire minimum jaar 2008.
Echter, bij het zee nabijgelegen Aeroparque Jorge Newbery zien we dat de temperatuur een bodem toont bij 2007, dus 1 jaar voor het sec. min. jaar 2008… en dat is precies wat kon worden verwacht want hetzelfde patroon is bij Buenos Aires zichtbaar in de vorm van een temperatuurdip 1 jaar voor de secundaire minima jaren 1965 en 1985.
https://data.giss.nasa.gov/cgi-bin/gistemp/stdata_show_v4.cgi?id=ARM00087582&dt=1&ds=14
Overigens, bij Aeroparque Jorge Newbery zien we duidelijke temperatuurdips bij de jaren 1964, 1987 en 2007… dus bij deze locatie draait het duidelijk om de secondaire minima; opnieuw valt hierbij op dat er geen sprake is van een consistente verschuiving van het faseverschil – ten als bij Buenos Aires.
Samengevat speelt het faseverschil bij Buenos Aires (+ de nabijgelegen locatie) duidelijk een minder grote rol en bovendien worden de temperatuur dips aangetroffen tijdens of zeer nabij zowel de primaire als secundaire minima (+ bij de nabijgelegen locatie betreft het enkel de secundaire minima).
Tokyo. Het is nogal willekeurig allemaal. Ruizig inderdaad; 5 jaar na ….., 4 jaar na …, 2 jaar na…, nog eens 2 jaar na…, 0, 1 jaar voor, …. 5 jaar voor ….. Waar zijn 3 jaar na, 1 jaar na, 2 jaar voor, 3 jaar voor, 4 jaar voor? De missende jaren zijn er bijna net zo veel als de genoemde jaren.
De Tokyo bodems komen niet overeen met de West-Europa bodems. Schijnt er een andere zon in Oost-Azië?
Overigens waarom telt de Groenland periode 1880-1950 niet mee? Toch de helft van de reeks. Kwam even niet uit?
Dan weer rondom primaire minima, dan weer rondom secundaire minima.
Faseverschil dat de andere kant op loopt. Het houdt niet op. Dus nogmaals, schijnt er een andere zon in Oost-Azië dan in West-Europa?
Al met al complete willekeur. Geen stabiel patroon in te herkennen.
Kijk eens aan, ook al geland in Buenos Aires! Alweer andere patronen! Ook daar schijnt weer een andere zon?
Alles bij elkaar is het nu al totale willekeur. En dan hebben we nog maar een paar locaties op de wereldbol aangedaan.
Allemenachies Martijn, toe redeneren naar een voor jou gewenste uitkomst breekt je uiteindelijk op. Zoveel is nu wel duidelijk.
Als je dit nog serieus wilt nemen, Martijn, dan zit er maar 1 ding op: kwantificatie van het vermeende patroon dat je ziet. Knoop er een correlatie getal aan vast en deel dat hier. Dan pas ben je wetenschappelijk goed bezig. Mijn advies? Begin er maar niet aan. Je kon wel eens een illusie armer worden: de zon is veel minder belangrijk dan jij wenst. (Ps. Waarom wens je dat eigenlijk?) Wel dapper geprobeerd hoor!
Temperatuur dips Christchurch (Nieuw Zeeland):
1911 (= 1 jaar voor primair minimum jaar 1912)
1930 (= 3 jaar voor primair minimum jaar 1933)
?
1976 (= primair minimum jaar 1976)
1992 (= 4 jaar voor primair minimum jaar 1996)
https://data.giss.nasa.gov/cgi-bin/gistemp/stdata_show_v4.cgi?id=NZM00093780&dt=1&ds=14
Net als bij Buenos Aires ook hier weer een onregelmatig fase verschil (zonder een duidelijk patroon van verschuiving).
Net als bij Groenland manifesteren de temperatuur dips bij Nieuw Zeeland zich duidelijk voorafgaand of bij de primaire minima jaren… mogelijk dat de primaire minima meer dominant worden bij het naderen van de polen…???
En nog twee van de zuidpool zelf:
* Temperatuur dips Mawson:
1962 (= 3 jaar voor secundaire minimum jaar 1965)
1982 (= 3 jaar voor secundaire minimum jaar 1985)
=> 1993 (= 3 jaar voor primair minimum jaar 1996)
=> 2015 (= 2 jaar voor primair minimum jaar 2017)
https://data.giss.nasa.gov/cgi-bin/gistemp/stdata_show_v4.cgi?id=AYM00089564&dt=1&ds=14
Kortom, overgangen van respectievelijk: 20, 11 en 22 jaar… dus de lengte van de tussenliggende periodes is duidelijk ook weer aan de zonnecyclus gerelateerd.
Ook hier weer een geringe dynamiek rond het fase verschil… maar wel een zeer duidelijk stabiel faseverschil t.o.v. zowel de primaire als secundaire jaren.
Het lijkt onderdeel te zijn van een patroon waarbij de verschuivende fase verschillen zich vooral op het noordelijk halfrond manifesteren; wellicht dat dit te maken heeft met dat de motor van het oceaan systeem zich op het zuidelijk halfrond begeeft bij de zuidpool waardoor daar de faseverschillen geen dynamisch verloop tonen???
* Temperatuur dips van Base Orcadas (dit betreft een locatie nabij het schiereiland van de zuidpool op een eiland midden in de zuidzee):
1930 (= 3 jaar voor primaire minimum jaar 1933)
1949 (= 5 jaar voor primair minimum jaar 1954)
1972 (= 4 jaar voor primaire minimum jaar 1976)
(Overgang van 19 jaar en 23 jaar)
=> 1915 (= 3 jaar na primaire minimum jaar 1912)
=> 1959 (= 6 jaar voor secundair minimum jaar 1965)
=> 1980 (= 5 jaar voor secundair minimum jaar 1985)
(Overgang van 44 jaar en 21 jaar)
https://data.giss.nasa.gov/cgi-bin/gistemp/stdata_show_v4.cgi?id=AYM00088968&dt=1&ds=14
Ook hier weer op het zuidelijk halfrond geen duidelijke verschuiving in de dynamiek rond het fase verschil.
De faseverschillen zijn bij dit laatste voorbeeld bij de zuidpool echter wel dusdanig groot dat de relatie met de zonneminima lastig hard te maken is omdat de temperatuur dips zich hier feitelijk rond de zonnemaxima aandienen. Enkel de lengte van de periodes ertussen vormt een hint dat er wel een verband is met de 22-jarige zonnecyclus.
Hierbij kan nog worden opgemerkt dat ook bij Groenland sprake is van een relatief groot fase verschil… dus de omvang van het faseverschil kan ook te maken hebben met de afstand tot de evenaar… waar de invloed van de zonnestraling het grootste is.
Echter, bij de polen is de invloed van de magnetische cyclus veel groter dan bij de evenaar… en aangezien het poloïdale magnetische veld van de zon een halve zonnecyclus uit fase loopt t.o.v. de TSI… zou hier wel eens de verklaring in kunnen liggen dat de temperatuur dips zich bij de polen meer in de buurt van de TSI maxima voordoen.
(De puzzelstukjes liggen nog niet helemaal op hun plek… maar het beeld van de puzzel is in grote lijnen nu al wel duidelijk zichtbaar, lijkt mij)
Re: “Schijnt er een andere zon in Oost-Azië?”
Nee, maar daar is wel sprake van een andere oceaan stroom.
Overigens, je weet toch ook dat de noord atlantische stroom er voor zorgt dat Europa relatief sterk is opgewarmd? Kortom, wanneer we praten over lokale patronen voor locaties die relatief dicht bij de zee liggen dan vormen de cycli binnen de oceaanstroom ook een factor om rekening mee te houden.
PS. Ik heb mijn eerste reisje rond de wereld inmiddels gemaakt en hierbij is een duidelijk verschil waargenomen rondom de verschillen tussen het noordelijk en zuidelijk halfrond: enkel bij het noordelijk halfrond lijken de patronen zich in 1 richting te verschuiven terwijl bij het zuidelijk halfrond veeleer sprake is van fluctuaties. Ook is duidelijk geworden dat de fase verschillen groter zijn bij de polen… vermoedelijk omdat daar de invloed van zonnemagnetisme groter is en het daarom niet alleen om de TSI draait. Vooral de periodes tussen de temperatuur dips verraden dat de zon erbij betrokken is.
De fase verschillen kunnen vast wel worden verklaard via een combinatie van het oceaan systeem + de invloed van het poloïdale magnetische veld van de zon, welke groot is wanneer de TSI laag is, zie:
http://klimaatcyclus.nl/klimaat/pics/solar-polar-field-strength-plus-solar-angular-momentum-and-speed-of-sun-relative-to-barycenter.jpg
Ja Martijn, …….. vast wel …….. maar voorlopig zie ik in je reacties toch vooral heel veel vraagtekens……..
Klopt Ronald, mijn observaties betreffende de lokale data heb ik enkel uitgewerkt voor de combinatie van de Bilt en Centraal Engeland, zie:
http://klimaatcyclus.nl/klimaat/pics/de-Bilt-%5BKNMI%5D-en-Central-England-%5BHadCET%5D-gemiddeld-temperatuurverschil-voor-jaren-rond-secundair-zonneminimum.jpg
Mijns inziens is dit resultaat eigenlijk al wel heel indrukwekkend… maar het roept natuurlijk wel de vraag op in hoeverre voor locaties elders in de wereld soortgelijke plaatjes ontstaan maar dan waarschijnlijk met een faseverschil t.o.v. de zonneminima jaren zelf.
Logischerwijs moet het toeval zijn dat er bij ons in West-Europa geen sprake is van een faseverschil met de zonneminima want anders zou dit beeld veel duidelijker zichtbaar moeten zijn bij de mondiale temperatuur data – met de kanttekening dat ik zo”n plaatje voor de LISIRD bijvoorbeeld überhaupt nog niet heb gemaakt.
Kortom, er valt nog heel veel uit te zoeken… maar ik voel er eigenlijk weinig voor om me in deze fase nog verder in de lokale data te gaan verdiepen.
Voor de discussie rondom mijn artikel betreft dit onderwerp in mijn ogen niet meer dan een verkenning aan de randen van de context; bovendien is al duidelijk dat het patroon dat ik in het artikel heb beschreven sterker zichtbaar is in de zeewateroppervlaktetemperatuur… dus de lokale data valt eigenlijk zelfs geheel buiten deze context.
@Ronald:
De IPCC-Summary for Policymakers is inderdaad niet relevant?
De onzekerheden worden beslist niet benadrukt.
In de beta-wetenschap maakt men gebruik van internationaal vastgestelde en herleidbare eenheden; het kalendergedoe voldoet er niet aan.
“global temperature” ook niet
“Global warming” wel degelijk!
“What’s in a name”?
“global warming” gaat over de “global mean temperature”
@Ronald:
Je zeurt.
Speciaal voor de lieden die meenden dat het verhaal niet zou werken wanneer alle jaren in beschouwing worden genomen:
Ik heb de impact van de correctie eens structureel doorgerekend voor de verschillende perspectieven (de correctie is hierbij telkens ge-finetuned op 4 cijfers achter de komma op basis van de gemiddelde waarde van de correlatie bij de primaire en secundaire waarden). Met de gebruikte rekentechniek kan dit eigenlijk maar worden doorgerekend t/m het 9-jarige gemiddelde rond de minima omdat bij het 11-jarige gemiddelde bij diverse periodes 1 of 2 jaar overlap ontstaat waardoor de correctie een deel van de impact verliest – met als gevolg dat de waarde enkel bij het 11-jarig gemiddelde duidelijk hoger ligt dan bij de kortere minima periodes.
Het resultaat is opmerkelijk stabiel (met correctie waarden tussen 0,114-0,142 W/m2 ):
http://klimaatcyclus.nl/klimaat/pics/LISIRD-TSI-vs-HadSST3-values-for-solar-minimum-years-plus-3Y-5Y-7Y-9Y-and-11Y-average-minima.jpg
Dit zijn de 2 meest opvallende patronen die zichtbaar zijn bij alle perspectieven in de hierboven vermelde nieuwe illustratie:
– het is opvallend dat in alle TSI en HadSST3 perspectieven (inclusief het 11-jaren perspectief) de eerste 5 waarden allemaal onder de laatste 5 waarden liggen;
– bovendien levert bij alle TSI en alle HadSST3 perspectieven (inclusief het 11-jaren perspectief) het jaar 1912 de laagste waarde op bij de eerste 5 waarden en levert het jaar 1976 de laagste waarde van de laatste 5 waarden.
beste Martijn,
Een goede wetenschapper geeft ook altijd een vergelijkingspunt, maar dat mis ik hier. Hoe goed is de correlatie tussen temperatuur en C02 voor diezelfde jaren? En waarom stop je in 1985? Het broeikaseffect begint pas rond die periode, dus je lijkt de meest relevante periode te willen ontwijken…
Re: 7horses “Een goede wetenschapper geeft ook altijd een vergelijkingspunt, maar dat mis ik hier.”
Voor mij is niet duidelijk waarom je dit punt hier ter sprake brengt.
De illustratie met de 6 perspectieven presenteer ik hier als een uitbreiding van de context die in het artikel wordt beschreven.
In het artikel wordt o.a. voor het perspectief van de 3-jarige periodes rond de minima beschreven dat CO2 geen bijdrage levert aan de verklaarde variantie voor de periode t/m 1984-86 niet verhoogd; zie deze informatie in paragraaf IV:
“• CO2:
– Volledige periode: R = 0,92; R-kwadraat = 0,84 (verklaarde variantie = 84%); p=0,000
– Periode t/m ’80s: R = 0,66; R-kwadraat = 0,44 (verklaarde variantie = 44%); p=0,037”
Je stelt dat het broeikaseffect “pas rond die periode” begint maar zo eenvoudig ligt het beslist niet want hierover bestaat geen consensus. Prof. Guido van der Werf gaat er bijvoorbeeld vanuit dat de impact van CO2 ook een significante bijdrage heeft geleverd aan de opwarming in de eerste helft van de 20ste eeuw. Maar ik begrijp je punt wel want ik weet dat er zelf ook geluiden zijn dat de impact van CO2 zich pas duidelijk in de jaren ’90 zou heeft gemanifesteerd… maar hier staat wel tegenover deze zienswijze op gespannen voet staat met de aantasting van de ozonlaag welke vanaf 1979 ook voor enige opwarming heeft gezorgd. In mijn artikel wordt voor het 3-jarige perspectief rond de minima beschreven dat de combinatie van de zon (TSI) en de ozonproblematiek (via de omvang v/h gat in de ozonlaag bij de zuidpool) maar liefst 96% van de variantie verklaard voor de periode rond de minima van 1890 en 2017.
Kortom, in mijn artikel is de periode na 1985 nadrukkelijk wel geheel behandeld.
De reden waarom ik met de nieuwe illustratie enkele de periode rond de minima over de periode 1890-1985 in beeld breng hangt direct samen met het feit dat juist in deze periode de impact van de zon het meest duidelijk zichtbaar is. Immers, de betreffende periode toont de bekende oscillerende bewegingen waarbij de statistiek in dit geval bij zowel de primaire minima als de secundaire minima (+ de combinatie van beide met de beschreven correcties) laat zien dat er relatief weinig ruimte is voor andere invloeden.
7horses, zie ook o.a. deze passage in de introductietekst:
Plus deze tekst in paragraaf IV:
Het was al besproken in het december artikel, maar de analyse kan inmiddels zowel verder worden aangescherpt als vereenvoudigd:
LISIRD TSI totale zonnestraling en HadSST3 zeewateroppervlaktetemperatuur correleren hoger tijdens de minima dan tijdens de maxima. De individuele fasen van de zonnecylus tonen ook een aanzienlijk hogere correlatie, metname wanneer hierbij rekening wordt gehouden met de 22-jarige cyclus, zie:
http://klimaatcyclus.nl/klimaat/pics/LISIRD-TSI-vs-HadSST3.jpg
“Op 2 juni 2020 heb ik hem en email hierover gestuurd. Vanaf die dag weet hij dus ZEKER dat hij ook naar die andere datasets moet kijken om tot correcte conclusies te komen.”
En wie ben jij dan wel?
Tot zover ben je enkel een idioot met een ban die hier met meerdere namen zijn mening blijft opdringen.
Hoi Nikos,
Ik zal zelf ook nog even reageren op de passage in de post van B.P. (die inmiddels is verwijderd) die je citeert.
Blijkbaar is het B.P. ontgaan dat in het artikel in paragraaf VIII wel degelijk wordt toegelicht waarom de aandacht is gevestigd op de LISIRD TSI data set:
Overigens, Greg Kopp is bepaald geen “klimaatscepticus” want hij behoort tot de toponderzoekers van het LASP die al decennia nauw samenwerkt met Judith Lean, die een sleutelrol speelt bij de PMOD. Hierbij kan ook nog worden opgemerkt dat In de LISIRD volgens Kopp noodzakelijke correcties zitten verwerkt die in andere data sets ontbreken.
Bovendien wordt in paragraaf VII een vergelijking gemaakt waarbij de 3 overige TSI data sets ook worden betrokken. Hier kan nog aan worden toegevoegd dat het bekend is dat vooral de periode voor 1950 geschikt is om de impact van de zon te bestuderen omdat daarna de invloed van de mens pas duidelijker een rol is gaan spelen; echter, voor 1880 worden de zeewateroppervlaktetemperatuur data als minder betrouwbaar beschouwd (ik heb in het februari artikel beschreven dat dit volgens de NASA ook geldt voor de mondiale temperatuur data sets, nadat ik in het december artikel op basis van een vergelijking met de PAGES 2K proxies zelf ook al tot die conclusie was gekomen).
De keuzes die ik heb gemaakt zijn dus wel degelijk zorgvuldig toegelicht.
Het is denk ik veelzeggend dat B.P. de indruk probeert te wekken dat een onderzoek gericht op de LISIRD TSI data set als “frauduleuze pseudowetenschap” probeert af te schilderen want hij is blijkbaar niet in staat om te herkennen dat het hier gaat wellicht om de beste data set die voor de experts beschikbaar is; Greg Kopp beschrijft dit op zijn eigen webpagina met deze woorden:
PS. Hans Labohm heeft mij overigens keurig op de hoogte gehouden van de inhoud wanneer er posts van B.P. werden verwijderd uit deze discussie; dit is vandaag ook weer gebeurd.
Bas Post is weer terug en heeft blijkbaar nog steeds niet geleerd dat je met drammerig gedrag en beledigingen niet ver komt.
Het lijkt erop dat Henk dJ weer eens onder een valse naam is opgestaan om zijn evangelische boodschap te verkondigen.
Hoi Willem,
Ik heb zelf de indruk dat Henk dJ inhoudelijk (veel) beter op de hoogte is dan B.P.
Met Henk d.J heb ik afgelopen zomer constructieve interacties kunnen voeren wat mij indertijd in mijn proces verder vooruit heeft geholpen (met de kanttekening dat dit toendertijd wel nog de fase betrof voordat de zon centraal kwam te staan in mijn analyse).
Meer specifiek: de fase voordat de zon in relatie tot de opwaarts gerichte klimaat oscillatie centraal kwam te staan in mijn analyse.
Hoi Martijn,
Ik kwam dit artikel tegen van Geli Wang, Peicai Yang & Xiuji Zhou: “Identification of the driving forces of climate change using the longest instrumental temperature record”
https://www.nature.com/articles/srep46091
Misschien ken je het artikel al wel, maar anders wellicht interessant om te lezen.
Mooi vondst Willem, dank!
Ik was me al wel bewust van de sterke parallel tussen de CET (Central England Temperature) en de mondiale temperatuurontwikkeling; in meerdere artikelen heb ik hieraan gerefereerd.
Heb in de discussies ook al eens beschreven dat de secundaire TSI minima duidelijk zijn terug te vinden in de CET en de temperatuurreeks voor de Bilt (terwijl op basis van de 11-jarige cyclus wordt dit fenomeen gemakkelijk over het hoofd gezien)… dus ook dit onderzoek uit 2017 bevestigd mijns inziens de relevantie van mijn vondst want het bevestigd dat de 22-jarige cyclus meer van belang is dan de 11-jarige cyclus.
PS. Toevalligerwijs staat voor morgen een nieuw (korter) artikel in de planning voor dit platform, waarin de kern van mijn onderzoek voor het eerst in een format wordt gepresenteerd dat geschikt is voor een peer reviewed publicatie (hierin wordt o.a. een bron uit 2008 gepresenteerd die beschrijft dat sinds het Maunder minimum de koudste fase van de 22-jarige cyclus wordt aangetroffen bij het minimum waarbij de polariteit positief is en ik presenteer zelf in het nieuwe artikel nu voor het eerst een temperatuurprofiel voor zowel de 22-jarige cyclus als de 11-jarige cyclus).
@ Martijn en Willem
Het is allemaal gewoon guido,die al meer dan een jaar met tientallen namen zijn mening op blijft dringen terwijl hij een ban heeft.
De meeste klimatologen hebben er geen moeite mee om aangepaste datasets te gebruiken (homogenisatie uit armoede, niet op basis van weloverwogen, controleerbare aanpassingen door apparatuurverschillen).
Martijn heeft weloverwogen een dataset gebruikt.
Niets mis mee.
Bas_nogwat heeft een bord voor z’n kop.
(Ik zou het ook in een volzin kunnen omschrijven, de conclusie is evenwel dezelfde)
Tsja Boels, onder het motto ‘hoge bomen vangen veel wind’:
Bas (Postedomme) & Ronald lijken inmiddels hard op weg om dikke ‘vrinden’ te worden.
Ze leven zich inmiddels al 2 weken heerlijk uit op de Engelse versie van mijn artikel:
https://www.sciencetalks.nl/590-2/
PS. Ik doe inmiddels mijn best inhoudelijke opmerkingen van een gepast antwoord te voorzien, maar de insteek van beide anonieme heren drijft ook daar op een hoog gehalte aan retoriek die zeer herkenbaar is (de heer Post kwam kon het zelfs niet laten om een animatie met een machinegeweer animatie te presenteren, zie: 25 May 2020 at 22:02).
@Martijn van Mensvoort:
Alternatieve verklaringen zijn nooit welkom in een conservatief gezelschap.
En zeker niet in het wereldje van de gezapige beelschermwetenschap waar men hopt tussen natuurkunde en de gokwereld.
Beste Boels, ik las vandaag een artikel wat je anti-middelings-hart nog verder van streek zal brengen ;-)
https://rdcu.be/b4MNq
@Voorbijganger:
Dank!
Jammer dat AI alleen verbanden tussen getalletjes kan vaststellen en geen natuurkundige wetmatigheden.
Ik heb overigens niets tegen middelen als men de boven- en ondergrens niet laat verdwijnen door het statistische truukje van de “wet van de grote aantallen”.
Er is niets stochastisch aan het weer of het klimaat en dat komt o.a. door de hoek van de aardas; het temperatuurhistogram is daarom een tweekoppig monster.