De respons van CO2 op de temperatuur

Door Dirk Visser.

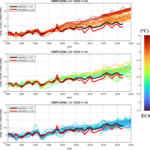
In dit artikel analyseer ik de respons van CO2 op temperatuurfluctuaties op een tijdschaal kleiner dan 10 jaar. Centraal in deze analyse staat het plaatje waarin HadCRUT5- en Mauna Loa-data getoond worden (figuur 1).

figuur 1. De gefilterde data van temperatuur (HadCRUT5)- en CO2 (Mauna Loa)-anomalieën. Nadere uitleg in de tekst.

Voor de temperatuur zijn de HadCRUT5-anomalieën gebruikt, dit zijn maandwaarden van de wereldgemiddelde temperatuuranomalie waaruit de seizoenscyclus is verwijderd. Verticale schaal is in graden Celsius. De gebruikte CO2-waarden van Mauna Loa zijn ook maandwaarden zonder seizoencyclus (in figuur 1 zijn deze waarden vermenigvuldigd met 0.28, het gebruik van deze factor resulteert in pieken van ongeveer gelijke hoogte). Verticale schaal in ppm. De periode loopt van 1960 tot 2022.

Op beide reeksen zijn de volgende filters gebruikt door middel van de volgende bewerkingen: 13-maands voortschrijdend gemiddelde (‘low pass’) en het signaal dat verkregen wordt door een 61-maands voortschrijdend gemiddelde af te trekken van het oorspronkelijke signaal (‘high pass’).

Er zijn drie opvallende zaken: de grote overeenkomst tussen de twee signalen, de verschuiving van CO2 ten opzichte van de temperatuur naar latere tijdstippen en het quasi-cyclische karakter van de pieken en dalen.

Correlatie tussen de twee reeksen geeft een maximum van de correlatiecoëfficiënt bij een verschuiving van 7.0 maanden, zie figuur 2 waarin ook een gefitte tweedegraads polynoom weergegeven is.

Figuur 2. Verticale as is de correlatiecoëffiënt, horizontale as de verschuiving in maanden tussen temperatuur en CO2 (CO2 terug in de tijd). De blauwe lijn verbindt de datapunten, de rode lijn is een gefitte tweedegraads polynoom.

De correlatie is doorgerekend tot een verschuiving van 450 maanden, figuur 3. Na de eerste piek bij 7 maanden treden op regelmatige afstanden pieken op in de correlatie, de 11de piek is bij maand 437. Hieruit blijkt dat de reeksen zich cyclisch gedragen met een cyclustijd van 43.0 maanden.

Figuur 3. Voortzetting van de correlatie getoond in figuur 1 tot 450 maanden verschuiving.

Uit fitten van  een eerstegraads polynoom tussen temperatuur (T) en 7-maands-verschoven CO2 (C) volgt:

C= 3.6T – 0.03, zie figuur 4.

We laten de constante 0.03 weg, C/T= 3.6 ppm/K.

We gebruiken K (Kelvin) als korte schrijfwijze van °C of graden Celsius.

Figuur 4. Scatterplot van CO2(min 7 mnd, verticale as) en temperatuur (horizontale as). De rode lijn is een gefitte eerstegraads polynoom. CO2= 3.6 * temperatuur – 0.03.

De interpretatie van figuur 1 is als volgt: er zijn twee sterke CO2-fluxen die in het algemeen met elkaar in evenwicht zijn: enerzijds de fotosynthese met een geschatte grootte van 60 ppm/jaar, anderzijds plantrespiratie en decompositie met elk een geschatte grootte van 30 ppm/jaar. Temperatuurfluctuaties verstoren dit evenwicht. Deze fluctuaties zijn in verband te brengen met de ENSO. Het is opvallend dat het onderliggende patroon een grote regelmaat vertoont, nadere toelichting in voetnoot (1). De respons op deze verstoringen gedraagt zich niet als een die flux-gedomineerd is, in dat geval zou de verschuiving in de tijd ongeveer 11 maanden moeten zijn (zijnde een faseverschuiving van 90 graden die in zo’n situatie optreedt). We veronderstellen dat deze verstoring te beschouwen is als een verstoring van een evenwichtssituatie. De volgende eenvoudige differentiaalvergelijking is dan een goede beschrijving van de situatie:

y’= a ( -y + b sin(qt)) 1

y is de CO2-anomalie, een accent geeft de afgeleide naar de tijd aan. De parameter a geeft aan hoe snel de evenwichtstoestand bereikt wordt, de term y geeft de afwijking van het evenwicht en de term b sin(qt) geeft de verstoring door de temperatuur. De parameter b is uitgedrukt in ppm per graad en de sinus heeft de amplitude van 1 graad. Samengevat: y’ is recht evenredig met y (de redelijke aanname is dat de natuur op lineair wijze naar evenwicht streeft) met daarbij een periodieke verstoring.

De oplossing van deze vergelijking is:

y= b sin(qt – arctg(p))/√(p² + 1) + c e^(-t/a)          met p= q/a 2

Omdat we geïnteresseerd zijn in de situatie bij dynamisch evenwicht (t naar oneindig) vervalt de term c e^(-t/a).

Er zijn twee limiet-gevallen: p= 0  (langzame cyclus) dan is

y= b sin(qt) 3

er is geen faseverschuiving tussen de twee signalen.

Voor p → ∞ (snelle cyclus) is:

y= ab/q sin(qt – pi/2) 4

De faseverschuiving is pi/2 rad = 90 graden. Er bestaat geen evenwichtssituatie, de temperatuurafhankelijke flux wordt niet beperkt door het bereiken van evenwicht. Uitdrukking 4 kan ook geschreven worden als y= -ab/q cos(qt) en is te beschouwen als oplossing van de vergelijking y’= ab sin(qt). Dit is de vergelijking 1 met weglating van de term –y.

Met de uit de analyse verkregen getallen bepalen we de waarden van a, b, p en q. De faseverschuiving arctg(p) is: 360*7/43= 58.6 graden.

q=2pi/(43 mnd)

p= tg(2pi *  7/43)= 1.64

zodat √(p² + 1) = 1.92

b= 3.6 * 1.92= 6.9 ppm/K

a= q/p= 2pi * 12/(43 * 1.64)= 1.07/jaar.

Er moet een correctie van 1.04 toegepast worden op de verkregen respons b= 6.9 ppm/K, zie voetnoot (1).

Dus de responstijd op temperatuurfluctuaties is 0.935 jaar en de grootte van de respons is b= 6.9/1.04= 6.6 ppm/K.

Voor een langzame stijging van de temperatuur (p is klein) geldt formule 3.

De stijging van de temperatuur van 1.5 graden in de afgelopen 150 jaar  kan dan hooguit een CO2-stijging in de atmosfeer van 1.5 x 6.6= 9.9 ppm veroorzaakt hebben.

Dit zou de respons zijn van voornamelijk de vegetatie op de temperatuur maar ook de respons van het oceaanoppervlak zal hierbij een rol spelen. Bij hogere temperatuur gaat de decompositie van plantaardig materiaal sneller. De responstijd van ongeveer 1 jaar is kort, zeker vergeleken met de responstijd van de oceanen. Dat is dus niet de respons van het oceaanoppervlak maar betreft het gehele volume van de oceanen, de thermohaliene circulatie is hierbij betrokken. Die responstijd is in de orde van 1000 jaar (zie voetnoot (2)). Uit Vostok-data blijkt (en ook uit directe metingen van lucht-watermonsters) een respons van 16 ppm/K.

Met behulp van formule 4 kunnen we een schatting maken hoe groot de huidige respons van CO2 in de atmosfeer zou zijn afkomstig van de oceanen zonder verdere CO2-bronnen. De waarden van a en b zijn bekend,  sin(qt – pi/2)/q benaderen we met de ruime schatting van een lineaire stijging van de temperatuur van 1.5 graden over 150 jaar: 0.5*1.5*150= 112.5 K jaar. De respons zou dus 112.5*16/1000= 1.8 ppm zijn.

In figuur 5 vergelijken we de wereldgemiddelde seizoencyclus van de temperatuur en van CO2. Voor CO2 nemen we de Mauna Loa data (de amplitude is iets groter dan de wereldgemiddelde, locatie is op 19 graden NB). Voor de temperatuur nemen we de GISTEMP Seasonal Cycle: amplitude 1.9 K, maximum in juli. Hoewel de zonintensiteit in januari 6.9% sterker is dan in juli (excentriciteit van de aardbaan) valt het maximum van de temperatuur in juli. CO2 begint in juni te dalen, dan is de zonintensiteit (dus ook de fotosynthese) op het noordelijk halfrond het sterkst. Beide effecten hebben te maken met het feit dat het meeste landoppervlak en vegetatie op het noordelijk halfrond ligt.

Uit figuur 5 blijkt dat CO2 daalt als respons op stijgende temperatuur (in feite daalt CO2 voornamelijk als respons op de zonintensiteit op het noordelijk halfrond, die loopt enkele weken voor op de temperatuur), de fotosynthese heeft de overhand op plantrespiratie en decompositie. Onderlinge correlatie geeft het volgende resultaat: verschuiving iets meer dan 3 maanden met een correlatiecoëfficiënt van -96%. Dit is dus een fluxgedomineerde respons (faseverschuiving is 90 graden).

Uit figuur 4 blijkt ruwweg een respons van -3/2 ppm/K, dit gebruiken we in formule 4 samen met q=2pi/jaar zodat de dynamische respons is: ab= -9.4 ppm/(K jaar). Omdat de Mauna Loa niet representatief is voor het wereldgemiddelde zal de werkelijke waarde lager zijn, een ruwe schatting is -6 ppm/(K jaar).

Voor langere tijdschalen dan de jaarlijkse cyclus is het voorstelbaar dat bij de stijgende temperatuur zoals in de laatste decennia (die mede te danken is aan sterkere zoninstraling) de respons van CO2 (bij afwezigheid van externe CO2-bronnen) dalend zou kunnen zijn. Extrapolerend naar nog langere tijdschalen kan (gebrek aan) fotosynthese een verklaring bieden voor de Holocene temperature conundrum (temperatuurdaling bij toenemende CO2).

Figuur 5. Seizoencyclus van mondiaal gemiddelde CO2 (groene lijn, hiervoor zijn Mauna Loa data genomen) en de mondiaal gemiddelde temperatuur (GISTEMP, rode lijn). De verticale as is zowel in ppm als in graden Celsius.

Conclusie en samenvatting: de respons van CO2 op temperatuurvariaties op zowel korte als lange tijdschalen is hooguit in de orde van 10-16 ppm/K. Als die temperatuurvariaties verband houden met variaties in zoninstraling kan de respons negatief zijn.

***

Voetnoten.

(1)

Het regelmatig patroon van figuur 3 heeft te maken met het gekozen filter. In figuur 6 is het tijdsdomein van het filter weergegeven. Rond de periode van 4 jaar is de doorlaatfactor groter dan 1, dat wil zeggen dat deze componenten door het filter versterkt worden. Bij de periode van 43 maanden is die factor 1.04, daarvoor wordt gecorrigeerd. Het filter laat goed de componenten met perioden tussen 2 en 8 jaar door.

De HadCRUT5 file is 2095 maanden lang. Uit autocorrelatie met de gefilterde data blijkt dat het cyclische patroon over de gehele periode naar voren komt. Periodiciteit: 44 +/- 1 maanden. Dit komt goed overeen met de periodiciteit van de ENSO, in de periode 1900-2024 waren er ongeveer 30 El Niño gebeurtenissen.

Figuur 6. Het gebruikte filter in het tijdsdomein. De rode lijn is het 13-maands ‘low pass’ filter, de groene lijn is het 61-maands ’high pass’ filter. De zwarte lijn is het gecombineerde filter. De grijze verticale lijn markeert de periode van 43 maanden.

(2)

Het volume van de oceanen is 1.335* 10^18 m3, de vorming van Arctisch en Antarctisch bodemwater is 48 Sv (1 Sv (Sverdrup) is 10^6 m3/s). Die twee getallen op elkaar delen geeft 846 jaar.

***